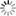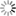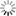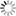nested_fista

General Description:

Nested FISTA method for solving problems of the form

$\min_x \left \{ \varphi(f(x))+\lambda g(Ax) \right \}$

Assumptions:

all functions are convex
$\varphi: {\mathbb R}^m \rightarrow {\mathbb R}$ - Lipschitz, nondecreasing and proximable
$f=(f_1,f_2,\ldots,f_m): {\mathbb R}^n \rightarrow {\mathbb R}^m$ . The components f₁,f₂,...,f_m are smooth
g - proper closed and proximable
A - linear transformation
$\lambda$ - positive scalar

Available Oracles:

function value of $\varphi$
prox of a positive constant times $\varphi$
function value of f (returns an m-dimensional column vector)
transposed Jacobian of f (an nxm matrix containing in its columns the gradients of each of the component functions)
function value of g
prox of a positive constant times g
value of the linear transformation A
value of the adjoint of A

Usage:

out               = nested_fista(Phifun,Phifun_prox,Ffun,Ffun_grad,Gfun,Gfun_prox,Afun,Atfun,lambda,startx,[par])
[out,fmin]        = nested_fista(Phifun,Phifun_prox,Ffun,Ffun_grad,Gfun,Gfun_prox,Afun,Atfun,lambda,startx,[par])
[out,fmin,parout] = nested_fista(Phifun,Phifun_prox,Ffun,Ffun_grad,Gfun,Gfun_prox,Afun,Atfun,lambda,startx,[par])

Input:

Phifun - function handle for phi

Phifun_prox - function handle for the proximal mapping of phi times a positive constant

Ffun - function handle for f

Ffun_grad - function handle for the transposed Jacobian of f

Gfun - function handle for g (if g is extended real-valued, it is enough to specify the operation of g on its domain)

Gfun_prox - function handle for the proximal mapping of g times a positive constant

Afun - function handle for the linear transformation A
Atfun - function handle for the adjoint of the linear transformation A

lambda - positive scalar

startx - starting vector

par - struct containing different values required for the operation of nested_fista

 field of par  possible values  default  description
  max_iter   positive integer  1000 maximal amount of iterations
 print_flag true/false   true true - internal printing is enabled
 Lstart positive real  1 an initial value for the outer Lipschitz
constant
 eta  real>1  2 multiplicative constant used when regretting
or backtracking
 stuck_iter  positive integer  100 maximal allowed number of iterations without
improvement
 inner_eps  positive real  1e-5 stopping criteria tolerance for the inner
fdpg method 
 inner_max_iter  positive integer  50 maximal number of iterations for the inner
fdpg method
inner_Lstart   positive real  1 initial value for the Lipschitz constant for
the inner fdpg method

Output:

out   - optimal solution (up to a tolerance)
fmin     - optimal value (up to a tolerance)
parout   - a struct containing containing additional information related to the convergence. The fields of parout are:

iterNum - number of performed iterations

funValVec - vector of all function values generated by the method
LvalVec - vector of all used Lipschitz constants

Method Description:

Employs an extension of the monotone version of FISTA for solving

$\min_x \left \{ \varphi(f(x))+\lambda g(Ax) \right \}$

using the following update scheme:

$\begin{array}{ll} z^k &= {\rm argmin}_{x \in {\mathbb R}^n}\left \{ \varphi(f(y^k)+\nabla f(y^k)^T(x-y^k))+\lambda g(Ax)+\frac{M_k}{2}\|x-y^k\|^2\right \}\\ x^{k+1} &\in {\rm argmin} \{ \varphi(f(x))+\lambda g(Ax) : x=x^k,z^k\},\\ t_{k+1} &=\frac{1+\sqrt{1+4t_k^2}}{2},\\ y^{k+1} &=x^{k+1}+\frac{t_k}{t_{k+1}}(z^k-x^{k+1})+\left (\frac{t_k-1}{t_{k+1}} \right )(x^{k+1}-x^k).\end{array}$

where M_k is chosen by a certain backtracking procedure. The vector z^kis a solution of an optimization problem that is solved by fdpg. The method stops when at least one of the following conditions hold: (1) the number of iterations exceeded par.max_iter (2) no improvement in function values was obtain in the past par.stuck_iter iterations.

Example 1:

Consider the problem

$\min_{x \in {\mathbb R}^{400}} \left \{ \max \left \{ x^T A_1 x+b_1^T x, x^T A_2 x+b_2^T x \right \}+\|Bx+c\|_1 \right \}$

where A₁,A₂,b₁,b₂,B,c are generated by the following commands.

>> randn('seed',329);

>> n=400;

>> m=200;

>> A1 = randn(n,n);

>> A1 = A1*A1';

>> b1 = randn(n,1);

>> A2 = randn(n,n);

>> A2 = A2*A2';

>> b2 = randn(n,1);

>> B = randn(m,n);

>> c = randn(m,1) ;

Note that A₁,A₂ are positive semidefinite by the way they are generated. We can now run nested_fista by noting that the problem at hand fits the main model with

$\begin{array}{ll} \varphi(y) &= \max\{y_1,y_2\},\\ f_1(x)&=x^T A_1 x+b_1^T x,\\f_2(x)&=x^T A_2 x+b_2^T x,\\ \lambda &=1,\\g(y) &= \|y+c\|_1,\\ A&=B. \end{array}$

The optimal solution is obtained by running the following commands.

>> f=@(x) [x'*A1*x+b1'*x; x'*A2*x+b2'*x];

>> grad_f = @(x) [2*A1*x + b1,2*A2*x + b2] ;

>> phi= @(x) max(x) ;

>> g = @(x) norm(x+c,1);

>> [xf,fun_xf,parout ] = nested_fista ( @(x) phi(x) , @(x,lamda) prox_max(x,lamda), @(x) f(x) ,@(x) grad_f(x),...

@(x) g(x) ,@(x,lamda) prox_l1(x+c,lamda)-c,@(x) B*x,@(x) B'*x, 1,ones(n,1)) ;

*********************

nested-fista

*********************

#iter fun. val. L val. inner L val. inner iternu.

1 41120.358535 2048.000000 262144 50

2 19911.092737 2048.000000 131072 50

3 10551.248162 2048.000000 65536 50

4 6076.307291 2048.000000 32768 50

5 3628.100774 2048.000000 16384 50

6 2219.251422 2048.000000 8192 50

7 1376.900043 2048.000000 4096 50

: : : : :

831 117.349390 2048.000000 8 2

832 117.349390 2048.000000 8 2

833 117.349390 2048.000000 8 2

834 117.349390 2048.000000 16 2

835 117.349390 2048.000000 8 2

836 117.349390 2048.000000 8 2

Stopping because of 100 iterations with no improvement

----------------------------------

Optimal value = 117.349390

Example 2:

Consider the problem of finding a point in the intersection of 5000 balls of dimension 200

$\|x-c_i\| \leq r_i, i=1,2,\ldots,5000$

where the centers and radii are generated by the commands

>> randn('seed',315);

>> rand('seed',315);

>> n=200;

>> m=5000;

>> x_true=randn(n,1);

>> r_all=[];

>> c_all=[];

>> for k=1:m

>> r=rand;

>> r_all=[r_all;r];

>> d=randn(n,1);

>> d=d/norm(d);

>> c=x_true+0.9*r*d;

>> c_all=[c_all,c];

>> end

To solve the problem, we first formulate it as the following minimization problem.

$\min_{x \in {\mathbb R}^{200}} \sum_{i=1}^{5000} [\|x-c_i\|^2-r_i^2]_+$

This model fits the main model with

$\varphi(y) = \sum_{i=1}^{5000} [y_i]_+, f(x) = \begin{pmatrix} \|x-c_1\|^2 -r_1^2 \\ \|x-c_2\|^2-r_2^2\\ \vdots \\ \|x-c_{5000}\|^2-r_{5000}^2 \end{pmatrix}, g(x)\equiv 0, A=I$

To solve the problem using nested_fista, we will exploit the following formulas:

${\rm prox}_{\alpha \varphi}(y) = {\mathcal T}_{\frac{\alpha}{2}}\left ( y-\frac{\alpha}{2}e \right ), \nabla f(x) = 2 \begin{pmatrix} x-c_1 & x-c_2 & \cdots & x-c_{5000} \end{pmatrix}$

where ${\mathcal T}_{\beta}$ is the soft-thresholding operator (also implemented in the function prox_l1) and e is the vector of all ones. With the above formulas in mind, we can solve the problem.

>> phi=@(y)sum(pos(y));

>> prox_phi=@(x,a)prox_l1(x-a/2,a/2);

>> f=@(x)(sum_square(x*ones(1,m)-c_all)-(r_all.^2)')';

>> grad_f=@(x)2*(x*ones(1,m)-c_all);

>> [xf,fun_xf,parout ] = nested_fista ( @(x) phi(x) , @(x,a) prox_phi(x,a), @(x) f(x),...

@(x) grad_f(x), @(x)0 ,@(x,a)x,@(x) x,@(x) x, 1,zeros(n,1)) ;

*********************

nested-fista

*********************

#iter fun. val. L val. inner L val. inner iternu.

1 283431.366571 16384.000000 256 50

2 71260.317218 16384.000000 128 50

3 9347.554536 16384.000000 64 50

4 89.325227 16384.000000 32 50

5 89.325227 16384.000000 16 50

989 0.000000 16384.000000 5.684342e-14 2

990 0.000000 16384.000000 2.842171e-14 2

991 0.000000 16384.000000 2.842171e-14 2

992 0.000000 16384.000000 2.842171e-14 2

993 0.000000 16384.000000 5.684342e-14 2

Stopping because of 100 iterations with no improvement

----------------------------------

Optimal value = 0.000000

The obtained solution is a good reconstruction of the vector x_true

>> norm(x_true-xf)

ans =

3.6669e-04