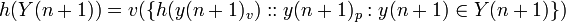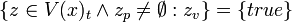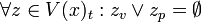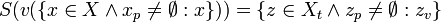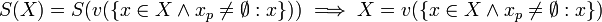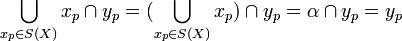Symbolic Logic:Programming:Value Set Proof
Contents |
[edit] Set Membership Equivalence
[edit] Proof
Firstly  is a Value Set because,
is a Value Set because,
- A1 is true
- A3
- A4
is,
simplifies to,
which is true,
Secondly using A2,
so every Value Set Y with S(Y) = Y must equal 
[edit] Functions of a Value Set
The following theorem gives the function on a value set of a type using the function of the type.
- (B1)
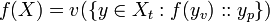
[edit] Proof
Let,
firstly we need to prove that K satisfies the axioms of a Value Set, if X is a value set,
[edit] Step 1
To prove that axiom A3 holds,
so,
[edit] Step 2
From (A4) applied to X,
which implies,
Which is (A4) applied to K.
[edit] Step 3
As  obeys the definition of a Value Set now prove that it equals
obeys the definition of a Value Set now prove that it equals 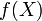 . Let
. Let 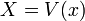 .
.
From A6,
From A1,
which implies,
so,
but also by simplifying,
so from A2,
gives,
[edit] Function of Multiple Parameters
If F is a value set of functions on a value set of a values,
- (B2)
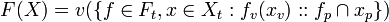
Let,
firstly we need to prove that K satisfies the axioms of a Value Set, if X is a value set,
[edit] Step 1
To prove that axiom A3 holds,
so,
gives,
which is A3 applied to K.
[edit] Step 2
From (A4) applied to F and X,
combining them,
gives,
as,
then
which is A4 applied to K.
[edit] Step 3
As  satisfies the definition of a Value Set now prove that it equals
satisfies the definition of a Value Set now prove that it equals  .
Let
.
Let 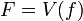 and
and 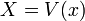 . Then
. Then 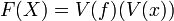 .
.
From A6,
From A1,
which implies,
so,
but also,
so from A2,
so,
[edit] Function of Vector of Parameters
If x is a vector, and X is a vector of Value Sets (representing multiple parameters) then,
- (B4)
![F(X) = v(\{ f(x_v)::\bigcap_{j \in J} x_p[j] : x\in X \}) \!](../w/images/math/a/e/1/ae1c62730114fb145296aef6ff5f018f.png)
[edit] Proof
Use induction. Firstly B1 gives the case for a scalar (n = 1).
Assume that B4 holds for a vector of size n then prove it holds for a vector of size n+1. Start with,
- (B3)
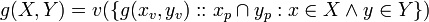
Let  be a scalar and
be a scalar and 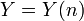 is a vector of size n. Also let
is a vector of size n. Also let 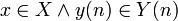 .
.
Let,
then,
and,
Also let,
in,
- (B3)
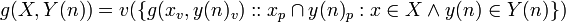
becomes,
Which is B4 for n+1, so by induction B4 holds for any number of parameters >= 1.
[edit] Assertions on Value Sets
- (C1)
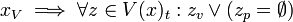
[edit] Proof
From A5
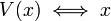
And,
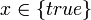 .
.
Using,
- (A1)
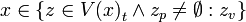
gives,
and,
or,
[edit] Pruning Empty Worlds
- (C2)

also,
which simplifies to,
so using A2,
[edit] Resolution
The standard form for Possible Worlds is defined as,
Then the resolution rule is,
If  ,
,  and
and  are a Value Sets, where
are a Value Sets, where
then,
[edit] Proof
therefore,
but,
so,
[edit] Links
- Symbolic Logic:Programming:Value Set
- Symbolic Logic:Programming:Value Set Programming
- Symbolic Logic:Programming
- Intelligence and Reasoning

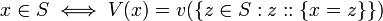
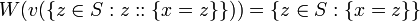


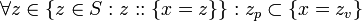
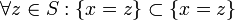

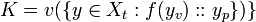

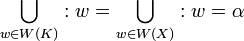
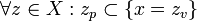

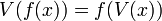



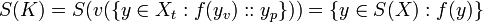

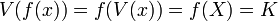
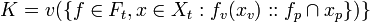




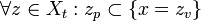
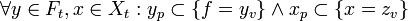


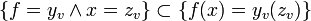


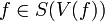
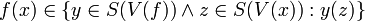
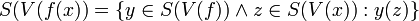
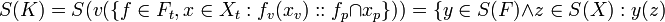

![y(n+1)_v = [x_v|y(n)_v] \!](../w/images/math/d/f/8/df8f87c9008b1f15137000297e6f96c4.png)
![y(n+1)_p = [x_p|y(n)_p] \!](../w/images/math/a/2/c/a2c1ea2c2e493d3b186690ac43c75f37.png)
![\bigcap_{j \in [1..n+1]} y(n+1)_p[j] = x_p \cap \bigcap_{j \in [1..n]} y(n)_p[j] \!](../w/images/math/9/b/5/9b5274dda609dd299c36f01045e92fdd.png)
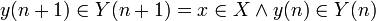
![g(X, Y(n)) = h([X|Y(n)] = h(Y(n+1)) \!](../w/images/math/0/7/2/0729ccf410fb3f668af93e9934a15e71.png)
![g(x_v, y(n)_v) = h([x_v|y(n)_v]) = h(y(n+1)_v]) \!](../w/images/math/9/2/3/923fba71ecc60aba0f79f02cdc282f29.png)