Chemical Physics

Theoretical Background

Overview: Chemical Kinetics

Rate Law

We will begin this discussion with a general description of reactions, rates and rate laws. We will discuss a general reaction:

$$aA + bB \rightarrow dD + eE$$

As the reaction occurs, the concentrations of the reactants and the products change. The rate of the reaction can be characterized by any of the following:

$$rate = -{1\over a} {d[A]\over dt}= -{1\over b} {d[B]\over dt}= {1\over d} {d[D]\over dt}= {1\over e} {d[E]\over dt}$$

These equations define the reaction rate. The reaction rate is defined in terms of the rate of change of concentration for any of the reaction components, divided by the stochiometric coefficient for that component. Stochiometric coefficients are positive for products and negative for reactants.

The reaction rate is dependent on the concentrations of chemical species involved in the reaction as follows:

$$rate = k[A]^p[B]^q$$

This equation is the rate law of the reaction. The proportionality constant, k, is known as the rate constant of the reaction. The rate constant depends on temperature, and more specifically it increases with it. The exponents in the rate law are integers (positive or negative) or simple fractions. These exponents are determined experimentally.

Reaction Order

The exponents of the concentration terms in equation (3) are the orders of the reaction with respect to each component of the reaction. For example, p is the order of the reaction with respect to the concentration of component A. If p is zero, the rate of reaction is independent of the concentration of A. The sum of the exponents is the overall order of the reaction.

Initial Rate Method

By measuring the change in concentration of one of the components of the reaction system with time, one can collect rate information. This data can be used to determine the initial rate of the reaction, which is the rate before concentrations of components have changed considerably. By taking the natural logarithm of Equation (3), one gets an expression relating the rate to the rate constants and concentrations of the reaction components:

$$ln(rate) = lnk + pln[A] + qln[B]$$

The natural logarithms of the concentrations of the individual reaction components are multiplied by the reaction order for that component. By measuring the initial rate of the reaction while changing the initial concentration of one of the reaction components, one can determine the order of the reaction with respect to that component. This is done by plotting the natural logarithm of the initial reaction rate versus the natural logarithm of the initial concentration of the varying component (all other initial concentrations are held constant). This should result in a straight line of slope equal to the order for that component. This process can be repeated, varying concentrations of other individual components in the reaction system, to determine the order of the reaction with respect to all components.

Iodination of Acetone

When iodine is mixed with acetone, the following reaction occurs:

$$CH_3COCH_3 + I_2 \rightarrow CH_3COCH_2I + H^+ + I^-$$

An analogous reaction occurs between bromine and acetone. The reaction is quite slow in the pH range of 4-7, but it occurs quite rapidly if the pH is below 3 or above 8. This implies an acid or base dependence.

The rate law for a reaction cannot be predicted from the balanced equation for the reaction. The rate law can only be determined experimentally. This reaction has been found to be catalyzed by hydrogen ion. The reaction rate increases with the concentration of H⁺ in acidic solution or with the concentration of OH⁻ in basic solution. The rate law is assumed to have the form:

$$rate = -{d[CH_3C(O)CH_3] \over dt} = -{d[I_2]\over dt} = k[CH_3C(O)CH_3]^p[I_2]^q[H^+]^r$$

The concentrations of all species are given in moles/liter. The exponents, p, q, and r indicate the order of the reaction with respect to acetone, iodine, and hydrogen ion, respectively.

It has been found that the rate of halogenation of acetone is independent of the concentration of halogen, except at very high acidities. The rates of reaction with the different halogens (chlorine, bromine and iodine) are identical, within a few percent. These facts are consistent with the mechanism shown in Figure 1.

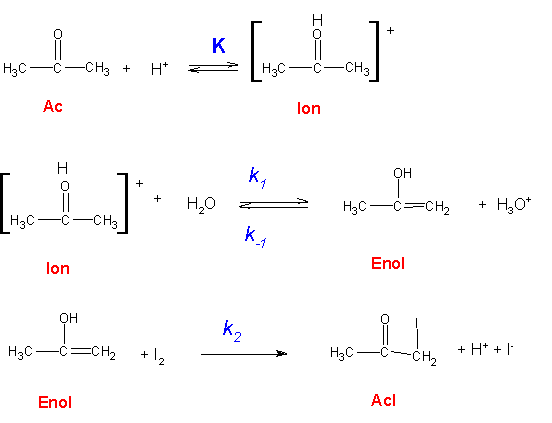
Since ketones are very weak bases, the equilibrium in the first reaction above is unfavorable for the formation of the ion. Under these circumstances [Ion] = K[Ac][H⁺], where K is the equilibrium constant for this reaction.

The rate equations for enol (Enol) and product (AcI) are, according to the mechanism:

$${d[Enol]\over dt} = k_1[Ion] - \left( k_{-1} [H^+] + k_2[I_2] \right) [Enol] \\ {d[AcI]\over dt} = k_2[I_2][Enol]$$

These rate equations may be solved for d[AcI]/dt under steady-state conditions by letting d[Enol]/dt = 0 and substituting [Ion] = K[Ac][H⁺]. This results in:

$${d[AcI]\over dt} = {k_1k_2K[Ac][H^+][I_2]\over k_{-1}[H^+]+k_2[I_2]} $$

This equation can be simplified if the enol that is formed in the second step reacts more rapidly with the halogen than with hydrogen ions; that is, k₂[I₂] >> k₋₁[H⁺].

$${d[AcI]\over dt} = k_1K[Ac][H^+] $$

This mechanism suggests that the over-all reaction is first-order in acetone and acid, but independent of the concentration of halogen.

Measuring the Reaction Rate by Absorption Spectroscopy

The Iodination of Acetone

The iodination of acetone is a particularly convenient and interesting reaction to study kinetically. The progress of the reaction is easily followed by directly observing the decrease in iodine concentration spectrophotometrically at a wavelength where none of the other reagents has significant absorption.

Reminder: Beer-Lambert Law

The Beer-Lambert law describes the absorption of light by matter. It states that the intensity of light after it passes through a substance is logarithmically related to the initial intensity of light. This relationship depends on the product of the absorption coefficient of the substance, α, and the distance the light travels through the material, l.

$$ I = I_0\cdot 10^{-\alpha l} $$

Here I is the measured light intensity, and I₀ is the initial light intensity. The absorbance, A, of light through a substance is defined as A = −log(I/I₀). In liquids, the absorption coefficient is a product of the molar absorptivity of the absorber, ε, and the concentration c of absorbing species, so that:

$$ A = \alpha l = \epsilon c l $$

Once ε and l are known, the Beer-Lambert law may be used the calculate the concentration of a solution by absorption spectroscopy.

Calculating the Reaction Rate

As will be confirmed in this experiment, the iodination reaction of acetone is of zero order for iodine (i.e., q in equation (6) is zero). In this experiment, acetone and acid will be present in large excess, and the iodine will be used in small concentrations to limit the extent of reaction. The small amount of iodine will be completely consumed, whereas the other reactants will remain at essentially constant concentration. Since the reaction rate is independent of the iodine concentration, the rate will be constant until all of the iodine is consumed. Under these conditions:

$$ rate = -{d[I_2]\over dt} = k \left[ CH_3C(O)CH_3 \right] ^p [H^+]^r = constant$$

A plot of [I₂] versus time is a relatively straight line; the slope is the reaction rate.

It is necessary to confirm that the exponent q is indeed zero. To do this, you will perform at least four experiments in which only the initial I₂ concentration differs. The slope of ln(rate) versus ln([I₂]_t=0) is the reaction order for I₂, q.

In order to get good results, at least four more experiments with different initial [CH₃C(O)CH₃] and three experiments with different initial [H⁺] should be performed. The order of the reaction p is determined from a plot of ln(k) versus ln([CH₃C(O)CH₃]_t=0). The slope of this plot is the reaction order for CH₃C(O)CH₃, p. The order of the reaction r is determined from a plot of the ln(k) of the rate of reaction versus the ln([H⁺]_t=o). The slope of this plot is the reaction order for H⁺, r.

The rate constant for the reaction can then be determined by the application of equation (6). A plot of the rate of reaction versus the product [CH₃C(O)CH₃]₀^p[H⁺]₀^r should be linear, and its slope is the rate constant for the reaction.