Wave equation (classical physics)

From Knowino

Jump to: navigation, search

In classical physics, the wave equation is the name given to a certain real partial differential equation in which the second derivative with respect to position x is proportional to the second derivative with respect to time t. Hence, the wave equation has the general form

$v^2 \frac{\partial^2 f(x,t)}{\partial x^2} = \frac{\partial^2 f(x,t)}{\partial t^2}.$

The real proportionality constant v² had dimension (length)² over (time)², i.e., v has the dimension of speed. In the simplest case v is independent of x and t (homogeneous space) and independent of f (no dispersion).

The wave equation can be generalized to three dimensions,

$v^2 \nabla^2 f(\mathbf{r},t) = \frac{\partial^2 f(\mathbf{r},t)}{\partial t^2} .$

The quantity v has again dimension of speed (length over time); ∇² is the Laplace operator; t is the time; r represents the space coordinates, r ≡ (x, y, z). In classical physics it is commonly the case that the function f(r,t) is real and observable. Examples of the meaning of f and v will be discussed below. In an isotropic space v does not depend on direction.

[edit] History

In 1727 John (Johann) Bernoulli studied the vibrations of a discrete number of masses connected by springs that satisfy Hooke's law. He derived a difference equation for the displacement ψ_k(t) of the kth mass as a function of time. In 1746 the work was extended by Jean Le Rond d'Alembert in his attack on the vibrating string problem typified by the violin string.^[1] To treat the continuous string d'Alembert increased the number of masses, letting their number go to infinity, while the size and mass of each individual "bead" went to zero, such that the mass density ρ of the string (mass per unit length) remained finite and constant over the string. In this manner d'Alembert derived the equation

$\frac{\partial^2 \psi(x,t)}{\partial x^2} = \frac{\rho}{T} \frac{\partial^2 \psi(x,t)}{\partial t^2},$

where T is the tension (force along the string, also taken constant over the string). He derived a solution of the form

$\psi(x,t) = f(x -v t) + g(x+vt)]\quad\hbox{with}\quad v \equiv \sqrt{\frac{T}{\rho}} .$

and emphasized that infinitely many curves f and g other than sinusoidal curves are modes of vibration. The 1747 article contains the first appearance of the wave equation in print. Note that the dimension of ρ/T is: M/L (M L/t²)⁻¹ = (t/L)², where the force T (mass times acceleration) has dimension ML/t². In total, ρ/T has indeed the dimension of one over speed squared.

[edit] Solution of the one-dimensional equation

Fig. 1 A non-periodic solitary wave traveling along x-axis to the right with constant speed v. At t=0 the wave is given by the function f(x) of x, at t=t₀ by f(x−vt₀), etc.

Any arbitrary differentiable function of the form f(x − vt) is a solution of the one-dimensional wave equation for constant (independent of x and t), real, and positive v. Hence any function f of x − vt may be called a wave. In contrast to what is often assumed, a wave (solution of the wave equation) does not have to be periodic, so that concepts like wave length and period are not necessarily defined. An example is given in Figure 1, where the red curve depicts an arbitrary wave propagating along the x-axis in positive direction. Snapshots at the times t=0, t=t₀, and t=2t₀ are depicted. At t=0 the red curve is the function f(x) that has non-zero values only in the neighborhood of x=0. At t=t₀ the red curve has the very same shape, but has non-zero values only in the neighborhood of x=vt₀. Note that the argument of f in the latter point on the x-axis is: x−vt₀ = 0.

In order to prove that f(x − vt) satisfies the wave equation, we write

$g: \mathbb{R}^2 \rarr \mathbb{R}\quad\hbox{with}\quad g(x,t)\; \stackrel{\mathrm{def}}{=}\; x- vt\,.$

It is to be shown that the product function

$h \equiv f\circ g\quad \Longleftrightarrow\quad h(x,t) \equiv f\big(g(x,t)\big) \equiv f\big(x-vt\big)$

is a solution of the wave equation for any real twice-differentiable function f of a single variable. Indeed, by the chain rule one gets,

$\frac{\partial h(x,t)}{\partial x} = \frac{d f(g)}{d g}\frac{\partial g(x,t)}{\partial x} = \frac{d f(g)}{d g}$

and

$\frac{\partial h(x,t)}{\partial t} = \frac{d f(g)}{d g}\frac{\partial g(x,t)}{\partial t} = - v\frac{d f(g)}{d g},$

and also

$\frac{\partial^2 h(x,t)}{\partial x^2} = \frac{d^2 f(g)}{d g^2}\quad \hbox{and} \quad \frac{\partial^2 h(x,t)}{\partial t^2} = (- v)^2\frac{d^2 f(g)}{d g^2} ,$

so that

$\frac{\partial^2 h(x,t)}{\partial x^2} = \frac{1}{v^2} \frac{\partial^2 h(x,t)}{\partial t^2},$

and it follows that h(x,t) ≡ f(x−vt) satisfies the wave equation.

The same steps can be followed for f(x + vt). Hence f(x±vt) satisfies the wave equation. In a notation less strict than just used—but notwithstanding obvious—this can be written as

$\frac{\partial^2 f(x \pm vt)}{\partial t^2} = v^2\frac{\partial^2 f(x\pm vt)}{\partial x^2}.$

Note that f(x+vt) for x=−vt has the same value as f(0) at t=0. In other words, the function moves along the negative x-axis.

The initial condition, the form f(x) of f at t = 0, specifies (partly) the wave. ^[2] Because f(x ± vt) differs from f(x) only by a translation of magnitude vt along the x-axis, (−vt in positive direction, +vt in negative direction), it is apparent that the function moves along the x-axis with velocity v, the velocity of wave propagation.

A general solution of the one-dimensional wave equation (first found by d'Alembert) is

$\psi(x,t) = f(x-vt) + g(x+vt)\,$

with

$\left[\frac{\partial^2 }{\partial x^2} - \frac{1}{v^2} \frac{\partial^2} {\partial t^2}\right] f(x-vt) = 0 \quad\hbox{and}\quad\left[\frac{\partial^2} {\partial x^2} - \frac{1}{v^2} \frac{\partial^2} {\partial t^2}\right] g(x+vt) = 0,$

where f and g are arbitrary twice differentiable functions of one variable.

In order to specify physical solutions the wave equation must be supplemented by boundary conditions. Let us impose the conditions:

$\psi(0, t) = 0,\quad \psi(L, t) = 0, \quad \forall t.$

When physically ψ(x,t) stands for the motion of a string of length L, this condition means that both ends of the string are clamped, which is the case for musical string instruments. In order to satisfy the boundary conditions, the functions f and g must be related by the equations

$f(-v t) + g(v t) = 0\quad \hbox{and}\quad f(L-vt) + g(L + vt) = 0, \quad \forall t.$

By putting f(u) = g(u) for all u ≡ vt and requiring f to be an odd function,

$f(-u) = -f(u) , \quad \forall u \in \mathbb{R},$

the first boundary condition is satisfied:

$f(-u) +g(u) = -f(u) + f(u) = 0\,.$

The second boundary condition enforces periodicity of f with wave length 2L

$f(L-vt) = -f(L+vt) = f(-L-vt)\quad \Longrightarrow\quad f(u+2L) = f(u),$

where the substitution vt = −(L+u) was made to obtain the expression after the arrow.

Notice that the part of f(x) lying between x = 0 and x = L is arbitrary, which corresponds to the physical fact that a string can be started vibrating from any shape whatsoever (subject to its ends being fixed). In particular, its shape need not be sinusoidal, proving that solutions other than the normal modes (to be discussed in the next section) can occur.

[edit] Normal modes of a string

The archetypal example of a wave is the transverse motion of a string constrained to vibrate in a plane. Let y(x,t) be the transverse displacement of the string from its equilibrium. The wave equation is

$\frac{\partial^2 y(x,t)}{\partial x^2} = \frac{1}{v^2} \frac{\partial^2 y(x,t)}{\partial t^2},$

where, as first shown by d'Alembert, the velocity v is √T/ρ. The tension T as well as the linear mass density ρ (mass per length) are constant over the string. The wave equation is derived under the assumption that the slope of the spring is small: $\partial y(x,t)/\partial x << 1$ . This holds if the maximum displacement of the spring is much less than its length.

The equation may be solved by a method known as separation of variables. One makes the Ansatz

$y(x,t) = F(x)\, G(t)$

where F depends on x only and G on t only. Substitution of the Ansatz into the wave equation gives

$G(t) \frac{\partial^2 F(x)}{\partial x^2} = \frac{F(x)}{v^2} \frac{\partial^2 G(t)}{\partial t^2} \quad\Longrightarrow\quad \frac{1}{F(x)} \frac{\partial^2 F(x)}{\partial x^2} = \frac{1}{v^2 G(t)} \frac{\partial^2 G(t)}{\partial t^2}.$

The equation on the right has a left-hand side solely depending on x, while its right-hand side depends solely on t. This can only be correct if both equations are equal to a constant, independent of x and t. Let us write −k² for this constant, where k may be complex in principle. We will, however, assume k to be real and hence will retrieve a restricted set of solutions, the normal modes. The wave equation separates into two equations,

$\frac{\partial^2 F(x)}{\partial x^2} = -k^2 F(x) \quad\hbox{and}\quad \frac{\partial^2 G(t)}{\partial t^2} = -(kv)^2 G(t).$

Clearly k has a dimension of reciprocal length and vk has a dimension of reciprocal time. It is common to write

$\omega \equiv vk$

and to call ω the angular velocity. Special solutions of the spatial and temporal equations are:

$\sin kx , \quad \cos kx \quad \hbox{and}\quad \cos \omega t,\quad \sin \omega t.$

General solutions are linear combinations of these functions.

Fig. 2. Fundamental mode, frequency ν₀.

Fig. 3. First overtone, frequency 2ν₀.

Fig. 4. Second overtone, frequency 3ν₀.

Fig. 5. Linear combination of lowest 3 modes

Let us next assume that the string is clamped for x = 0, that is, the displacement is zero for x = 0. This boundary condition excludes a cosine type solution, so that the spatial equation is of the form sinkx. If the string has length L and its end is also clamped, it follows that

$kL = n \pi\quad\hbox{for integer}\quad n.$

It is common to write

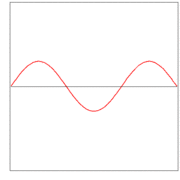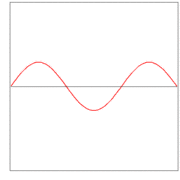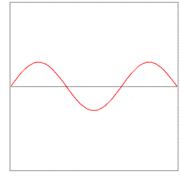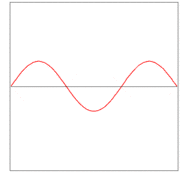
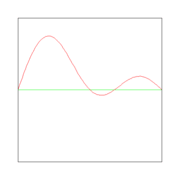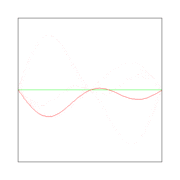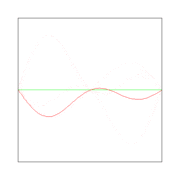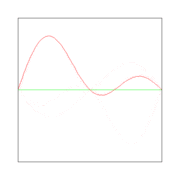
$k = \frac{n\, \pi}{L} \equiv \frac{2\pi}{\lambda}\quad\hbox{with}\quad \lambda = \frac{2\pi}{k} = \frac{2L}{n}.$

Here λ, a quantity with a dimension of length, is called wave length. In figures 2, 3. and 4: λ= 2L/1, 2L/2, and 2L/3, for the first vibration (the "fundamental"), the second (the "first overtone"), and the third (the "second overtone"), respectively. These sinusoidal modes of the string are its normal modes.

With regard to the temporal equation we remark the following. The string is pulled to certain shape y(x), held in position for a brief instant, and then let go at t = 0, so that dy/dt = 0 at t = 0 and dy/dt ≠ 0 for t > 0,

$\left(\frac{\partial y(x,t)}{\partial t}\right)_{t=0} = 0.$

This condition excludes the function sinωt, because the first derivative of the sine is the cosine which is not zero at t = 0. Hence the time function is of the form cosωt. In total, the solution with given boundary and initial conditions is

$y(x,t) = A \sin(k x)\cos(\omega t)\;.$

A function of this form is a standing wave. Clearly, this function repeats itself after a time period t₀ with

$t_0 = \frac{2\pi}{\omega} = \frac{2\pi}{k v} = \frac{\lambda}{v} = \frac{2L}{n} \sqrt{\frac{\rho}{T}},$

where T is the tension and ρ is the mass density. The reciprocal period is the frequency,

$\nu = \frac{1}{t_0} = \frac{\omega}{2\pi} = \frac{n}{2L} \sqrt{\frac{T}{\rho}} \equiv n \nu_0 ,$

where ν₀ ≡ 1/(2L) √T/ρ is the fundamental frequency.

One may wonder whether the solution has the general form found by d'Alembert and discussed in the previous section. Note to that end that

$\sin(k x)\cos(\omega t) = \frac{1}{2}\left[ \sin k(x+ v t) + \sin k(x-vt) \right],$

and that the sine function is odd, sin(−u) = −sin(u).

[edit] Examples

In figures 2, 3, and 4 are shown the functions

$y_n(x,t) = 0.3 \sin nx\cos n t\quad \hbox{for}\quad n=1,2,3,$

which implies the following choices: (i) the initial displacement (amplitude) A = 0.3, (ii) the length of the string L = π, (iii) the propagation velocity v = 1, and (iv) the radial velocity ω = kv = n. These choices are compatible: the choice of L fixes a unit of length and the choice of v fixes a unit of time; these units can be fixed independently. The d'Alembertian operator defined by

$\square^2 \quad \stackrel{\mathrm{def}}{=}\quad \frac{\partial^2}{\partial x^2} - \frac{1}{v^2}\frac{\partial^2}{\partial t^2}$

is linear. Hence

$\square^2 \Big(\sin x\cos t + 0.7 \sin 2x\cos 2 t + 0.5 \sin 3x\cos 3 t \Big) = 0.$

This solution of the wave equation is shown in figure 5.

[edit] Acoustical waves

To a very good approximation the propagation of pressure waves in a fluid (liquid or gaseous) medium is described by the wave equation. Such waves are called acoustical waves, because the propagation of sound in a medium is an example.

Consider an undisturbed fluid particle at position x and let its displacement, caused by a disturbance at time t, be in the z direction, so that after being disturbed the particle is at position: x + z(x,t). If the slope satisfies $\scriptstyle \partial z / \partial x << 1$ (the "acoustic approximation") the displacement z satisfies

$\frac{\partial^2 z(x,t)}{\partial x^2} = \frac{1}{\bar{v}^2} \frac{\partial^2 z(x,t)}{\partial t^2},$

where

$\bar{v}^2 = \left. \frac{dP(\rho)}{d\rho} \right|_{\rho_0}.$

Here ρ is the density of the fluid, ρ₀ the undisturbed density, and P(ρ) the pressure in the fluid.

If the fluid is air, then $\bar{v}$ is the speed of sound. There may be 3-dimensional motion in the general case, satisfying the 3-dimensional wave equation, with an appropriate modification of the parameters. However, if is the fluid is homogeneous and isotropic, the extension is without any difficulties.

[edit] Electromagnetic waves

In a region of space where the charge and current densities are zero, Maxwell's equations for the electromagnetic field in vacuum lead to

$\begin{align} \nabla^2 \mathbf{E}(\mathbf{r},t) &= \frac{1}{c^2} \frac{\partial^2 \mathbf{E}(\mathbf{r},t) }{\partial t^2} \\ \nabla^2 \mathbf{B}(\mathbf{r},t) &= \frac{1}{c^2} \frac{\partial^2 \mathbf{B}(\mathbf{r},t) }{\partial t^2} \\ \end{align}$

where E is the electric field and B is magnetic induction (also known magnetic flux density). The quantity c is the speed of light in vacuum. The vector potential A and the scalar potential φ give rise to both E and B through

$\begin{align} \mathbf{B}(\mathbf{r},t) &= \boldsymbol{\nabla} \times \mathbf{A}(\mathbf{r},t) \\ \mathbf{E}(\mathbf{r},t) &= -\boldsymbol{\nabla} \phi - \frac{1}{k}\frac{\partial \mathbf{A}(\mathbf{r},t)}{\partial t} \\ \end{align}$

where in SI units k = 1 and in Gaussian units k = c. Both A and φ satisfy wave equations (that hold in absence of charge and current densities); they are

$\begin{align} \nabla^2 \mathbf{A}(\mathbf{r},t) &= \frac{1}{c^2} \frac{\partial^2 \mathbf{A}(\mathbf{r},t) }{\partial t^2} \\ \nabla^2 \phi(\mathbf{r},t) &= \frac{1}{c^2} \frac{\partial^2 \phi(\mathbf{r},t) }{\partial t^2} \\ \end{align}$

[edit] Notes

↑ J. d'Alembert, Recherches sur la courbe que forme une corde tenduë mise en vibration [Researches on the curve formed by a stretched string set into vibration], Histoire de l’Académie des sciences et belles-lettres (Berlin) vol. 3, pp. 214–249 (1747, published 1749).
↑ Since the differential equation is of second order, a second initial condition, for instance the time derivative of f at t = 0, is required for the general solution of the wave equation.

[0] J. d'Alembert, Recherches sur la courbe que forme une corde tenduë mise en vibration [Researches on the curve formed by a stretched string set into vibration], Histoire de l’Académie des sciences et belles-lettres (Berlin) vol. 3, pp. 214–249 (1747, published 1749).

[1] Since the differential equation is of second order, a second initial condition, for instance the time derivative of f at t = 0, is required for the general solution of the wave equation.

[1]

[2]

Wave equation (classical physics)

Contents

[edit] History

[edit] Solution of the one-dimensional equation

[edit] Normal modes of a string

[edit] Examples

[edit] Acoustical waves

[edit] Electromagnetic waves

[edit] Notes

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Community

Toolbox