Triple product

From Knowino

Jump to: navigation, search

Parallelepiped spanned by vectors A, B, and C (shown in red).

In linear algebra, a triple product is a common term for a product of three vectors A, B, and C leading to a scalar (a number). The absolute value of this scalar is the volume V of the parallelepiped spanned by the three vectors:

$V = \big|\mathbf{A}\cdot(\mathbf{B}\times\mathbf{C})\big|,$

where B × C is the cross product of two vectors (resulting into a vector) and the dot indicates the inner product between two vectors (a scalar).

The triple product is sometimes called the scalar triple product to distinguish it from the vector triple product A×(B×C). The scalar triple product is often written as [A B C]. The vector triple product can be expanded by the aid of the baccab formula.

[edit] Explanation

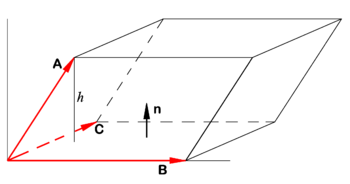
Let n be a unit normal to the parallelogram spanned by B and C (see figure). Let h be the height of the terminal point of the vector A above the base of the parallelepiped. Recall:

Volume V of parallelepiped is height h times area S of the base.

Note that h is the projection of A on n and that the area S is the length of the cross product of the vectors spanning the base,

$h = \mathbf{A}\cdot\mathbf{n}\quad\hbox{and}\quad S = | \mathbf{B}\times\mathbf{C}|.$

Use

$V = (\mathbf{A}\cdot \mathbf{n})\;(| \mathbf{B}\times\mathbf{C}|) = \mathbf{A}\cdot (\mathbf{n}\,| \mathbf{B}\times\mathbf{C}|) = \mathbf{A}\cdot (\mathbf{B}\times\mathbf{C}),$

where it is used that

$\mathbf{n}\; |\mathbf{B}\times\mathbf{C}| = \mathbf{B}\times\mathbf{C}.$

(The unit normal n has the direction of the cross product B × C).

If A, B, and C do not form a right-handed system, A•n < 0 and we must take the absolute value: | A• (B×C)|.

[edit] Triple product as determinant

Take three orthogonal unit vectors i , j, and k and write

$\mathbf{A} = A_1\mathbf{i}+ A_2\mathbf{j}+A_3\mathbf{k}, \quad \mathbf{B} = B_1\mathbf{i}+ B_2\mathbf{j}+B_3\mathbf{k},\quad \mathbf{C} = C_1\mathbf{i}+ C_2\mathbf{j}+C_3\mathbf{k}.$

The triple product is equal to a 3 × 3 determinant

$\mathbf{A}\cdot(\mathbf{B}\times\mathbf{C}) = \begin{vmatrix} A_1 & B_1 & C_1 \\ A_2 & B_2 & C_2 \\ A_3 & B_3 & C_3 \\ \end{vmatrix}.$

Indeed, writing the cross product as a determinant we find

$\begin{align} \mathbf{A}\cdot(\mathbf{B}\times\mathbf{C}) &= \mathbf{A}\cdot \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ B_1 & B_2 & B_3 \\ C_1 & C_2 & C_3 \\ \end{vmatrix} \\ &= \big(A_1\mathbf{i}+ A_2\mathbf{j}+A_3\mathbf{k}\big)\cdot \big[ (B_2\,C_3 - B_3\,C_2)\;\mathbf{i}+ (B_3\,C_1 - B_1\,C_3)\;\mathbf{j} + (B_1\,C_2 - B_2\,C_1)\;\mathbf{k} \big] \\ &= A_1\;(B_2\,C_3 - B_3\,C_2)+ A_2\;(B_3\,C_1 - B_1\,C_3) + A_3\;(B_1\,C_2 - B_2\,C_1)\\ &=\begin{vmatrix} A_1 & B_1 & C_1 \\ A_2 & B_2 & C_2 \\ A_3 & B_3 & C_3 \\ \end{vmatrix} . \end{align}$

Since a determinant is invariant under cyclic permutation of its columns, it follows

$\mathbf{A}\cdot(\mathbf{B}\times\mathbf{C}) = \mathbf{B}\cdot(\mathbf{C}\times\mathbf{A}) = \mathbf{C}\cdot(\mathbf{A}\times\mathbf{B}).$

[edit] Arbitrary basis

The fact that the triple product represents the volume of a geometric figure (a parallelepiped) suggests that it must be possible to express the volume with respect to any (even a non-orthonormal) basis.

In the derivation of a general equation for the volume, a minor change of notation is needed, since it is essential to distinguish a component vector (bold) from a geometric vector (arrow on top). The following substitutions are made:

$(\mathbf{i}, \;\mathbf{j}, \; \mathbf{k}) \rightarrow (\vec{e}_1, \; \vec{e}_2,\; \vec{e}_3) \quad\hbox{and}\quad (\mathbf{A}, \;\mathbf{B}, \; \mathbf{C}) \rightarrow (\vec{A}, \; \vec{B},\; \vec{C}).$

An arbitrary (possibly non-orthonormal) basis $\vec{a}_1, \, \vec{a}_2,\, \vec{a}_3$ of Euclidean 3-space is connected by a 3×3 non-singular matrix S to an orthonormal basis basis,

$(\vec{a}_1, \, \vec{a}_2,\, \vec{a}_3) = (\vec{e}_1, \, \vec{e}_2,\, \vec{e}_3) \mathbf{S}, \qquad \vec{e}_i \cdot \vec{e}_j = \delta_{ij}, \quad i,j=1,2,3.$

The representation g′ of the metric tensor with respect to the new basis becomes

$g'_{ij}:= \vec{a}_i\cdot\vec{a}_j = \sum_{k,\ell=1}^3 S_{ki} \; \vec{e}_k\cdot\vec{e}_\ell\; S_{\ell j} = \sum_{k,\ell=1}^3 S_{ki} \;g_{k\ell}\;S_{\ell j }.$

(It is exactly this equation that shows that the g_ij are the components of a tensor). Although the unprimed metric tensor g is represented by an identity matrix, it will be carried along. In matrix language

$\mathbf{g'} = \mathbf{S}^\text{T}\, \mathbf{g}\, \mathbf{S}\quad\Longrightarrow\quad g' = \det(\mathbf{S^\text{T}g S}) = \det(\mathbf{S})^2\; g \quad\Longrightarrow\quad \det(\mathbf{S}) = \pm \sqrt{\frac{g'}{g}},$

where the following two rules for determinants (numbers) were used

$\det(\mathbf{AB}) = \det(\mathbf{A})\det(\mathbf{B}), \quad \det(\mathbf{A}^\text{T})= \det(\mathbf{A})$

and the determinants of g and g′, are written as g and g′, respectively. From:

$\vec{A} = (\vec{e}_1, \, \vec{e}_2,\, \vec{e}_3) \begin{pmatrix} A_1 \\ A_2 \\A_3 \end{pmatrix} = (\vec{e}_1, \, \vec{e}_2,\, \vec{e}_3)\; \mathbf{S} \mathbf{S}^{-1} \; \begin{pmatrix} A_1 \\ A_2 \\A_3 \end{pmatrix}$

follows

$\vec{A} = (\vec{a}_1, \, \vec{a}_2,\, \vec{a}_3) \begin{pmatrix} A'_1 \\ A'_2 \\A'_3 \end{pmatrix} \quad\hbox{with}\quad \begin{pmatrix} A'_1 \\ A'_2 \\A'_3 \end{pmatrix} = \mathbf{S}^{-1}\begin{pmatrix} A_1 \\ A_2 \\A_3 \end{pmatrix}.$

Note that the component vectors A = (A₁, A₂, A₃) and A′ = (A₁′, A₂′, A₃′) represent the same geometric vector $\vec{A}$ . The same transformation rule holds for the components of the geometric vectors $\vec{B}$ and $\vec{C}$ . By design the three primed component vectors span the same parallelepiped as the original unprimed component vectors. In terms of matrices the transformation rule is,

$\begin{pmatrix} A_1' & B_1' & C_1' \\ A_2' & B_2' & C_2' \\ A_3' & B_3' & C_3' \\ \end{pmatrix} = \mathbf{S}^{-1} \begin{pmatrix} A_1 & B_1 & C_1 \\ A_2 & B_2 & C_2 \\ A_3 & B_3 & C_3 \\ \end{pmatrix} \quad \Longrightarrow\quad \det[\mathbf{A}'\; \mathbf{B}' \; \mathbf{C}'] = \pm\sqrt{\frac{g}{g'}}\; \det[\mathbf{A}\; \mathbf{B} \; \mathbf{C}]$

where the general rule

$\det(\mathbf{A}^{-1}) = \det(\mathbf{A})^{-1}$

is used.

This result shows that the generalized expression for the volume V (a real positive number, which is why absolute values are taken) of the parallelepiped

$V = \sqrt{|g|}\;\; \big\vert\det[\mathbf{A} \; \mathbf{B}\; \mathbf{C}]\,\big\vert$

is invariant under any basis transformation and represents always the volume of the same parallelepiped, irrespective of the choice of basis. If A, B, and C are the component vectors of $\vec{A},\; \vec{B},\; \vec{C}$ with respect to an orthonormal basis then g = I. The identity matrix has unit determinant, so that the earlier expression for the volume is indeed recovered as a special case.

[edit] Examples

The infinitesimal volume element dV spanned by the following three orthogonal vectors

$(\vec{e}_1, \, \vec{e}_2,\, \vec{e}_3) \begin{pmatrix} \text{d}x & 0 & 0 \\ 0 & \text{d}y & 0 \\ 0 & 0 & \text{d}z \\ \end{pmatrix}$

is equal to dV = dxdydx because g = I and the determinant of a diagonal matrix is equal to the product of the diagonal elements.

Similarly for spherical polar coordinates

$(\vec\mathbf{a}_\theta, \, \vec\mathbf{a}_\phi, \, \vec\mathbf{a}_r) = (\vec\mathbf{e}_x, \, \vec\mathbf{e}_y, \, \vec\mathbf{e}_z) \mathbf{S}$

with

$\mathbf{S} := \begin{pmatrix} \partial x/\partial \theta & \partial x/\partial \phi & \partial x/\partial r \\ \partial y/\partial \theta & \partial y/\partial \phi & \partial y/\partial r \\ \partial z/\partial \theta & \partial z/\partial \phi & \partial z/\partial r \\ \end{pmatrix} = \begin{pmatrix} \cos\phi & - \sin\phi & 0 \\ \sin\phi & \cos\phi & 0 \\ 0 & 0 & 1 \\ \end{pmatrix} \begin{pmatrix} \cos\theta & 0 & \sin\theta \\ 0 & 1 & 0 \\ -\sin\theta & 0 & \cos\theta \\ \end{pmatrix} \begin{pmatrix} r & 0 & 0 \\ 0 & r\sin\theta & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}.$

The metric tensor is

$\mathbf{g} = \mathbf{S}^\text{T} \mathbf{S} = \begin{pmatrix} r^2 & 0 & 0 \\ 0 & r^2\sin^2\theta & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}$

The volume element spanned by the following three orthogonal (non-unit) vectors

$(\vec\mathbf{a}_\theta, \, \vec\mathbf{a}_\phi, \, \vec\mathbf{a}_r) \begin{pmatrix} \text{d}\theta & 0 & 0 \\ 0 & \text{d}\phi & 0 \\ 0 & 0 & \text{d}r \\ \end{pmatrix}$

is equal to (vertical bars around the array indicate a determinant):

$\text{d}V = \sqrt{|g|} \; \begin{vmatrix} \text{d}\theta & 0 & 0 \\ 0 & \text{d}\phi & 0 \\ 0 & 0 & \text{d}r \\ \end{vmatrix} =\sqrt{r^4\sin^2\theta}\; \text{d}\theta\,\text{d}\phi\,\text{d}r = r^2\sin\theta\; \text{d}\theta\,\text{d}\phi\,\text{d}r$

Note that r²sinθ ≥ 0 for 0 ≤ θ ≤ π.

[edit] Reference

M. R. Spiegel, Theory and Problems of Vector Analysis, Schaum Publishing, New York (1959) p. 26

Triple product

Contents

[edit] Explanation

[edit] Triple product as determinant

[edit] Arbitrary basis

[edit] Examples

[edit] Reference

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Community

Toolbox