Surface (geometry)

From Knowino

Jump to: navigation, search

In common language, a surface is the exterior face of an object in space (a body), and is usually considered as part of that object.

Some examples of surfaces are:

The surface of a ball — called a sphere — is completely uniform.
The surface of a cube can be seen as six squares that are glued together along their edges.
The surface of a ring — called a torus — is markedly different from both the sphere and the cube because it has a "hole".
A piece of rock or mineral may be irregular, crumpled, distorted, but it still has a surface.

Starting from this intuitive idea, over the centuries, the mathematical notion – or rather: several related mathematical notions – of a surface has emerged.

The essential feature of a surface (as an abstract geometrical object) is its two-dimensionality: It has length and breadth, but no depth — and this is also the common property of the mathematical definitions.

Surfaces that are the face of a body are two-sided: They have an interior and an exterior side. Such surfaces are called orientable.
But not all abstract surfaces defined in mathematics can be interpreted as the outside hull of some body. Such surfaces are one-sided and are called non-orientable. A well-known example of a non-orientable surface is the Moebius strip.

Remark:
In higher-dimensional spaces (dimension ≥ 4) the term surface or hypersurface is used for higher-dimensional analogues of common surfaces.

[edit] Mathematical definitions

In analytic geometry and in differential geometry a surface can be described

explicitly by a real function of two variables

z = f (x, y)

and the surface is the graph of the function, i.e., the set of points

$\{ (x,y,f(x,y)) \in \mathbb R^3 \}$ ,

or it can be defined

implicitly by the zeroes of a function of three variables

F (x, y, z)

i.e., the surface consists of the points

$\{ (x,y,z) \mid F(x,y,z)=0 \}$ .

In topology a surface is defined as a topological space such that

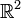every point has a neighbourhood that is homeomorphic to the (open) unit disk in $\mathbb R^2$ .

i.e., the space locally "looks" like a plane.

[edit] Mathematical example: the sphere

A sphere (with radius r) is implicitly given by

x 2 + y 2 + z 2 = r 2

using the function

F (x, y, z) = x 2 + y 2 + z 2 - r 2

.

An explicit form using the function

$f(x,y) = \sqrt { r^2 - x^2 - y^2 } \quad\text{for}\quad x^2 + y^2 \le r^2 \ ( x,y\in\mathbb R )$

is

$\left( x,y,\sqrt { r^2 - x^2 - y^2 } \right)$

which, however, only describes the upper half of the sphere.

Some content on this page may previously have appeared on Citizendium.

Surface (geometry)

[edit] Mathematical definitions

[edit] Mathematical example: the sphere

Personal tools

Namespaces

Variants

Views

Actions

Search

Navigation

Community

Toolbox