Symbolic Logic:Programming:Function to Fact Transformation
Functions treat the return value (result) differently from the parameters. The result is calculated from the parameters. There is no explicit variable into which the value will be entered.
In Demand Driven Evaluation we will show how the requested variable can be calculated from the other parameters (including the result). This makes the role return value equivalent to the parameters. As the return value is not necessary the value that is calculated, from a structural point of view it behaves in the same way as a parameter.
But the imperative programming languages that we will be building on do treat the return value differently from the parameters. There is no variable to contain the return value.
So to make this clear and precise we need a transformation of a function, that turns the return value into an extra parameter.
Contents |
[edit] Function Transformations
A call to a function looks like,
That is a function  is applied to some parameters
is applied to some parameters 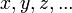 . Other forms of the function are needed in order to transform functions into the form required for Demand Driven Evaluation. The List Equivalent Function
. Other forms of the function are needed in order to transform functions into the form required for Demand Driven Evaluation. The List Equivalent Function  is,
is,
the inverse of this function is 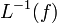 .
.
- D1
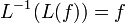
so,
The List Equivalent Function may be defined using Curried functions,
- D2

or,
- D2
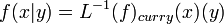
Lists are manipulated using,
- List prepend,
- List concatenation
Demand Driven Evaluation requires the result to be treated in the same way as paramaters. The Result Equivalent Function  is defined,
is defined,
- D3
![R(f)(x+[r]) \iff f(x) = r \!](../w/images/math/0/2/7/027b8dc0d488d10aca69f7d74936d579.png)
The goal is to transform expressions to equivalent forms as Result Equivalent Functions. For example to transform an expression.
The use of operators is syntactic sugar. Each of the operators could be replaced with functions,
and this function can be transformed into,
The goal is to transform this expression into,
This is the Result Equivalent Transformation (RET). This transformation is the subject of the next section.
For simplicity define 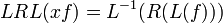 .
.
[edit] The Result Equivalent Transformation (RET)
Starting with a function call,
The List Equivalent Expression is,
where,
Using D3,
Both  and
and  could be either constants, variables, or calls to functions. If they are calls to functions they must be replaced by variables.
could be either constants, variables, or calls to functions. If they are calls to functions they must be replaced by variables.
Let,
or
and now a recursive pattern appears.
[edit] The RET Tuple
A data representing the state of process is recorded in the RET Tuple (RETT).
The RET Tuple has attributes,
- An expression

- On input, the input expresion being processed.
- On output the variable containing the result variable, or a constant or other variable.
- A RET expression
 .
.
The definition,
allows access to the components of an RETT.
The RET function takes an RETT as a parameter and returns a RETT as a result.
[edit] Rule 1
[edit] Rule 2
[edit] Rule 3
To be applied only if rule 1 cant be applied.
[edit] Simplified rule 1
If f is a constant or variable rule 1 simplifies down to,
[edit] Example
The example in Function Transformations is,
For readability define 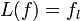 . Applying the RET function is,
. Applying the RET function is,
[edit] Step 1
Applying the simplified rule 1.
![(x, j_s \and R(equals_l)(j_c+[x])) \!](../w/images/math/2/5/a/25aa146f359dd2840b02d2247880d1ac.png)
- where,
![j = RET(([x, plus_l([power_l([y, 2]), 5])], true)) \!](../w/images/math/d/1/6/d1609b9315381d120f9cd0be26cdb5aa.png)
Applying rule 2 a couple of time and rule 3 once gives,
![(result, k_s \and R(equals_l)([x, k_c, result])) \!](../w/images/math/0/3/d/03d7d6973acd16150c621f296e940c58.png)
- where,
![k = RET((plus_l([power_l([y, 2]), 5]), true)) \!](../w/images/math/6/d/f/6df4c37216ba743b4aac71fec75f0651.png)
[edit] Step 2
To expand ![RET((plus_l([power_l([y, 2]), 5]), true)) \!](../w/images/math/1/8/8/1884debacb4837c2b578ffb9214c9692.png) apply the same process,
apply the same process,
![(result, k_s \and R(equals_l)([x, k_c, result])) \!](../w/images/math/0/3/d/03d7d6973acd16150c621f296e940c58.png)
- where,
![k = (a, m_s \and R(plus_l)([m_c, 5, a])) \!](../w/images/math/6/d/5/6d55ef666b188d860e17c13abbf61f68.png)
- and,
![m = RET((power_l([y, 2]), true)) \!](../w/images/math/3/1/f/31f4357307dbb1b76c12ceb4646ac584.png)
or,
![(result, m_s \and R(plus_l)([m_c, 5, a]) \and R(equals_l)([x, a, result])) \!](../w/images/math/e/c/7/ec76360239827e28943119536592ebd2.png)
- where,
![m = RET((power_l([y, 2]), true)) \!](../w/images/math/3/1/f/31f4357307dbb1b76c12ceb4646ac584.png)
[edit] Step 3
To expand ![RET((power_l([y, 2]), true)) \!](../w/images/math/5/7/8/5780570976ab2e5745870b5c25472bfb.png) apply the process again,
apply the process again,
![(result, m_s \and R(plus_l)([m_c, 5, a]) \and R(equals_l)([x, a, result])) \!](../w/images/math/e/c/7/ec76360239827e28943119536592ebd2.png)
- where,
![m = (b, true \and R(power_l)([y, 2, b])) \!](../w/images/math/2/6/e/26e04a7bbe03fc89b1649af5d21d772a.png)
or,
This gives the Return Equivalent transformation of,
as,
with the returned value of 
[edit] Meta Mathematics
The RET function is described above as if it is a function when really it should be a meta function. The distinction is quite subtle.
The RET function is intended to a mathematical expression, and rearrange it to form another mathematical expression. But that is not quite what I have described. All I have done is write some new theorems that are implied by,
- D3
![R(f)(x+[r]) \iff f(x) = r \!](../w/images/math/0/2/7/027b8dc0d488d10aca69f7d74936d579.png)
To fix this problem I need,
- A way of representing a mathematical expression as something to be worked on.
- Some types (or sets) to which expressions can belong.
[edit] Mathematics as Data
The mathematics about mathematics idea is what has been come to be though of by meta mathematics. I wanted a short symbol to represent meta so I chose the greek letter  (eta). It is short and it rhymes with meta.
(eta). It is short and it rhymes with meta.
Writing mathematics as data is the inverse of writing mathematics about mathematics. So this is 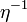 . This demotion of mathematics allows meta mathematics to be written. For example
. This demotion of mathematics allows meta mathematics to be written. For example
is an expression representing some mathematics, not the mathematics,
The difference can be seen in the types,
whereas,
The square brackets are used to indicate that 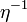 is not a function. It is a change of the meaning of the text between the square brackets.
is not a function. It is a change of the meaning of the text between the square brackets.
 is used to put variables into meta mathematics. For example, if,
is used to put variables into meta mathematics. For example, if,
then
[edit] Types for Meta Mathematics
| Type | Description | Example |
|---|---|---|
| expression | any mathematical expression | x2 * 5 |
| call | a call to a function | factorial(5) |
| variable | a variable (placeholder for a value) | x |
| constant | a constant value | 5,e,π,factorial as in the function name. |
| construction | a set or list construction | [5,6,7],{0,1} |
[edit] Rule 1
[edit] Rule 2
[edit] Rule 3
[edit] Links
- Symbolic Logic:Programming:Value Set Programming
- Symbolic Logic:Programming
- Intelligence and Reasoning


![L(f)([x, y, z]) = f(x, y, z) \!](../w/images/math/d/3/3/d33af6c0730e31366403e28a66d58806.png)
![g([x, y, z]) = L^{-1}(g)(x, y, z) \!](../w/images/math/1/6/c/16c70c05ee5a506736637850ca685d37.png)
![x|[a, b, c] = [x, a, b, c] \!](../w/images/math/8/9/7/897b776fead38247688475c519154c3b.png)
![[a, b, c]+[x, y] = [a, b, c, x, y] \!](../w/images/math/2/f/f/2ff7234a5fdeaf24aa977eb671fb01ba.png)
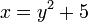

![L(equals)([x, L(plus)([L(power)([y, 2]), 5])]) \!](../w/images/math/b/b/d/bbde944196b84b1446caa3b811554205.png)
![R(L((equals))([x, b, result]) \and R(L((plus))([c, 5, b]) \and R(L((power))([y, 2, c]) \!](../w/images/math/b/7/7/b772e349d72fa3b21966cd8666b265cc.png)


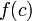

![c = [x, y, z ...] \!](../w/images/math/2/1/c/21cfca2ce65b591940ca2d9458983042.png)
![f(c) = R(f)(c+[true])\!](../w/images/math/8/a/b/8abb5bdb6b176f8cb2dfcf2d25e3738b.png)
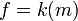
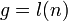
![R(x)(y+[true]) \and k(m)=x \and l(n)=y \!](../w/images/math/d/3/5/d355a91ffae241b8e720069480aeacc7.png)
![R(x)(y+[true]) \and R(k)(m+[x]) \and R(l)(n+[y]) \!](../w/images/math/e/f/7/ef7d834edfc0838a8901c67c5da09917.png)
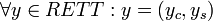
![RET((f(c), s)) = (x, y_s \and R(z_c)(y_c+[x])) \!](../w/images/math/5/1/3/513daac26f644ba68cf3175ee7b09b1f.png)





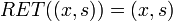
![RET((f(c), s)) = (x, y_s \and R(f)(y_c+[x])) \!](../w/images/math/d/d/0/dd064f244b3b59b12d4d5ae909c8a663.png)
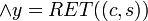
![L(equals)([x, L(plus)([L(power)([y, 2]), 5])]), \!](../w/images/math/1/a/2/1a22786e7e9073d9f4261a8b22b59c47.png)
![RET(equals_l([x, plus_l([power_l([y, 2]), 5])]), true) \!](../w/images/math/0/1/8/018773a706d79acd49f04c63418f41d1.png)
![(result, R(power_l)([y, 2, b]) \and R(plus_l)([b, 5, a]) \and R(equals_l)([x, a, result])) \!](../w/images/math/b/b/7/bb76b07d4b92f762a1a9261ffe3a56c4.png)
![equals_l([x, plus_l([power_l([y, 2]), 5])])\!](../w/images/math/8/b/e/8be706093b4f610d1f510870ad28ba62.png)
![R(power_l)([y, 2, b]) \and R(plus_l)([b, 5, a]) \and R(equals_l)([x, a, result]) \!](../w/images/math/d/7/2/d72500a37c613961af5dd4d567d95b52.png)
![\eta^{-1}[ x^2 + 1 = 0 ]) ] \!](../w/images/math/9/9/6/9962e5252513678f99d149923df03edb.png)
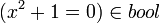
![\eta^{-1}[ x^2 + 1 = 0 ] \in expression \!](../w/images/math/7/e/5/7e522a959d0e06662b154047daf420c2.png)
![f = \eta^{-1}[sin] \!](../w/images/math/e/b/2/eb28f337acdd730723e5dd35c5ee560c.png)
![x = \eta^{-1}[\pi / 4] \!](../w/images/math/4/4/9/449093990a409ded500a818c05383892.png)
 ] = \eta^{-1}[sin(\pi / 4) ] \!](../w/images/math/2/a/b/2ab2da36f7a73d60b07bd13ba56bd1e4.png)

 ], s)) = (x, \eta^{-1}[ \eta[y_s] \and R(\eta[z_c])(\eta[y_c]+\eta[x]])]) \!](../w/images/math/a/4/9/a49cd1395e916afa542468e79f3c6c51.png)
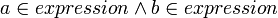
![RET((\eta^{-1}[\eta[a]|\eta[b]], s)) = (\eta^{-1}[ \eta[z_c]|\eta[y_c] ], y_s) \!](../w/images/math/2/e/5/2e530c88f03f3c6a88d328fb3a4eabdd.png)
