|
|
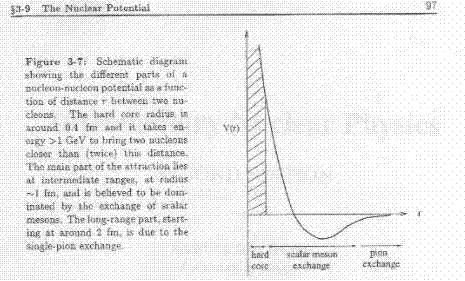

The first figure shows the
internucleon potential as a function of the distance [1].
The solid line of the second figure shows the
respective quantuty of the intermolecular force [2].
The impressive similarity between
these graphs is discussed in the following lines.
Nuclear data show that in nuclei having more than a very small number
of nucleons, the density of nucleons is about the same. The
force between two nucleons depends on the distance between their
centers. This force is characterized by a very hard core where
the force is repulsive. Outside this core, there is a
rapidly decreasing attractive force.*
These properties of nuclei correspond to what is found in a
liquid drop. The density is uniform and the dependence of the
van der Waals force on the distance between
the centers of two molecules resembles that of the nuclear
force.
The two figures show the near region where the force is strongly
repulsive. In both cases the repulsion stems from the Pauli exclusion
principle acting between identical fermions. The rapidly decaying
attractive force shows the residual nature of the van der Waals
and the nuclear forces. Two properties of an electromagnetic system
make a sufficient condition for the existence of a force
having a residual characteristics:
- the field is related to positive and negative charges whose
sum vanishes.
- The potential decreases like .
The regular monopole theory used for describing hadronic structure
satisfies these conditions and thereby, it
explains the residual nature of the nuclear force and
the success of the nuclear liquid drop model.
QCD does not satisfy the second requirement mentioned above and
it is not clear how can it provide an explanation for the residual
nature of the nuclear force. Indeed,
QCD is known for more than 3 decades. In spite of that,
textbooks on QCD do not provide an explanation for the
nuclear data described herein.
*There are other features of the nuclear force like tensor
components and spin-orbit interaction. For a discussion of the
nuclear tensor force and its sign , see the text
beginning at line 4 of p. 94 of the following article:
A Regular Monopole
Theory and Its Application to
Strong Interactions
(Published in Has the Last Word been Said
on Classical Electrodynamics?
(Rinton Press, NJ, 2004)).
References:
[1] S. S. M. Wong, Introductory Nuclear Physics (Wiley, New York,
1998). P. 97.
[2] H. Haken and H. C. Wolf, Molecular Physics and Elements of
Quantum Chemistry (Springer, Berlin, 1995). P. 15.
|
|
|
|

