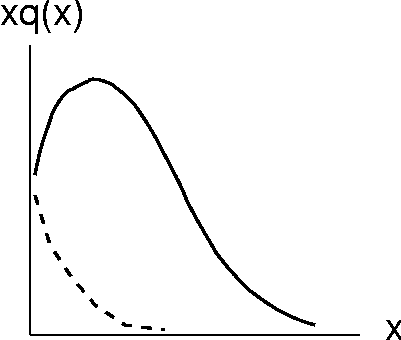|
|
Fig. 1. This figure describes qualitatively the
quantity xq(x) as a function of x (q(x) denotes
quark/antiquark distribution, respectively). The solid
line represents quarks and the broken line represents antiquarks.
(The original accurate figure can be found on p. 281 of
D. H. Perkins, Introduction to High Energy Physics
(Addison-Wesley, Menlo Park, CA, 1987).
The discussion carried out here relies on the data depicted in the figure
and compares the width of the quarks' and the antiquarks' graphs.
Evidently, the antiquarks data is confined within a smaller x-region.
Now, a higher x-width indicates a higher Fermi motion. Therefore,
in a nucleon, the Fermi motion of quarks is higher than that of antiquarks.
Thus, using the uncertainty principle, one concludes that, in a
nucleon, the volume occupied by an antiquark is larger than that of a quark.
The regular magnetic monopole theory easily explains this effect. The
explanation relies on the similarity between electrostatics
of charges and magnetostatics of monopoles. Thus, at inner regions of
the nucleon, the magnetic
field of the nucleon's core is not screened completely
by the quarks. Hence, antiquarks,
which have the same sign of magnetic charge as that of the nucleonic
core, are pushed towards outer regions of the nucleon.
It is not clear how can QCD explain this effect. Indeed, the small
energy level of π mesons indicates that the quark-antiquark force
is very strong. Moreover, the π meson's volume is smaller than that
of the proton. Hence, one wonders why the four QCD quarks (the three
valence quarks and the antiquark's companion) do not attract the
antiquark and confine it inside
a volume which is (at least) not larger than the
volume occupied by them. As a matter of fact, the data described
by figure 1 is known for several decades. In spite of this fact,
the issue presented on this page is not discussed in QCD textbooks.
|
|
|
|
