יחידה 2: t למדגמים בלתי-תלויים  >>  2.1: מבחן F לבדיקת שוויון שונויות

כמו שלמדנו בשיעור שעבר, אחת ההנחות הבסיסיות של מבחן t למדגמים בלתי תלויים היא שוויון שונויות.

במקום שרק נניח הנחה זו, אנו נבדוק אותה סטטיסטית. הבדיקה נעשית באמצעות מבחןF  לבדיקת שוויון שונויות (זו אחת הגרסאות של מבחן (F. בשנה הבאה תקדישו את מירב הזמן למבחן F במסגרת הקורס "ניתוח שונות".

מבחן  F  לשוויון שונויות

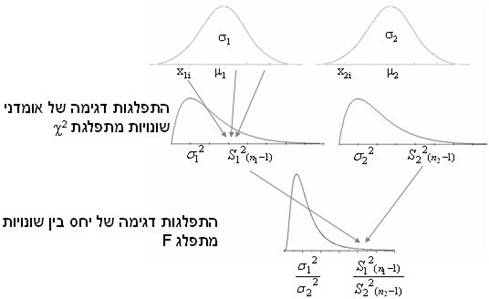
במבחן F אנו שואלים: אם שני מדגמים אכן לקוחים מהתפלגויות בעלות שונויות שוות, אנו נצפה שההבדלים שבין אומדני השונויות של שני המדגמים יהיו קטנים. ההבדל שביניהם נובע מטעות מקרית. אם ההבדל שביניהם גדול דיו, אנו נחשוש שהמדגמים לא לקוחים מהתפלגויות בעלות שונויות שוות ואז לא נוכל להניח שוויון שונויות במבחן t למדגמים בלתי תלויים.  

התפלגות הדגימה של אומדני השונויות תתפלג חי בריבוע כאשר התפלגות המשתנה נורמלית או כאשר . מומלץ לנסות ולבדוק כיצד נראית התפלגות דגימה של שונויות ב-applet של התפלגויות הדגימה שלמדנו בסוף סמסטר א': http://www.ruf.rice.edu/%7Elane/stat_sim/sampling_dist/index.html

היחס שבין שני אומדני השונויות יתפלג F כאשר אומדני השונויות מתפלגים חי בריבוע.

מכאן שהיחס שבין שני אומדני השונויות יתפלג F בשני המקרים שצוינו לעיל כאשר:

·         התפלגויות המשתנים נורמליות

או

·         בשני המדגמים .

הסטטיסטי    יחושב כיחס שבין האומדן הגדול חלקי האומדן הקטן מבין השניים.

שימו לב: ניתן לחשב גם את היחס ההפוך ולבדוק את המובהקות באמצעות טבלה נוספת.

שוב נבקש להזכיר שמבחן F משמש אותנו השנה (במקרה זה) כעזר בבדיקת ההנחות שבמבחן t למדגמים בלתי תלויים, אך עומד בפני עצמו כמבחן הבוחן האם שני מדגמים לקוחים מאוכלוסיות בעלות שונות שווה (ועל כך באופן נרחב בשנה הבאה בקורס....ניתוח שונות).

שלבים בביצוע מבחן F:

1.  הנחות:  דגימה מקרית, התפלגות הדגימה F.

2.  השערה:   

3.  רמת מובהקות:  

4.  בדיקת ההשערה:

, כאשר

 הן  דרגות החופש של .

מטבלת F או מ- EXCEL:

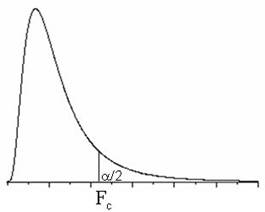
5.  מסקנה:  אם  או ש-  , נדחה את .

כאשר משתמשים במבחן F לבדיקת שוויון שונויות, כשלב מקדים למבחן t אנו "נשמח" אם לא נדחה את  (כי אנו מעדיפים/רוצים להניח שוויון שונויות במבחן t).

בדוגמא מהשיעור הקודם:

קבוצה 1:

קבוצה 2:

1.  הנחות:  דגימה מקרית, התפלגות הדגימה F.

2.  השערה:   

3.  רמת מובהקות:   

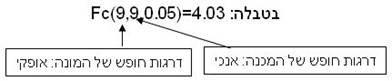
4.  בדיקת ההשערה:    

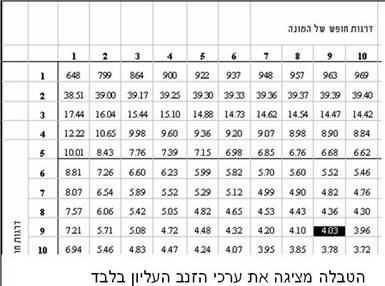
מהטבלה: 

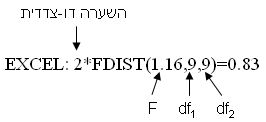
מ-EXCEL:

5.  מסקנה:  לא ניתן לדחות את  ולומר, ברמת בטחון של 95%, שהמדגמים לקוחים מאוכלוסיות בעלות שונויות שונות.

► חזור                    המשך ◄