Question 09/99
MEAN DEFLECTING FORCE
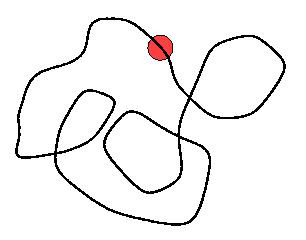
Consider a bead sliding without friction on a wire placed in a horizontal
plane and forming a closed loop. The force acting on the bead is always perpendicular
to the direction of its motion, to the right or to the left depending
the direction the wire is curving.
A force to the right or to the left, relative to the direction of the bead's
motion, is defined as positive or negative, respectively.
Let the mass of the particle
be m and its (constant) velocity v, while the length of
the wire loop is L.
(a) If the loop doesn't intersect itself,
what is the time average of the perpendicular force, and
how does it depend on the shape of the loop?
(b) What if the wire does cross itself?
(This means that parts of the loop
are slightly out of horizontal plane.)
This question was suggested by Y. Kantor. It was inspired
by Newton's first attempt to calculate centripetal force as it appears
in his "Waste Book" (dated 1664-1665).
Back to "front page"