Answer to the Question 08/99
ZEROTH ORDER RAINBOWThe question was:
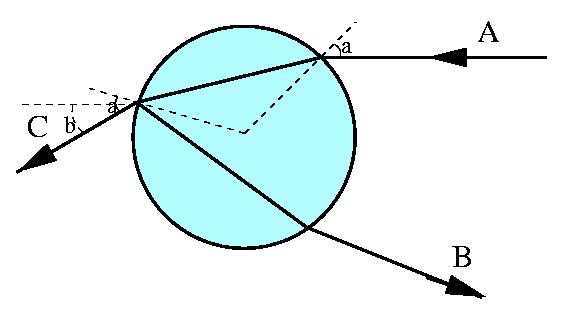
A ray of light coming from the sun (A) enters a water drop, is reflected internally once, and exits in direction B. The angle of maximal intensity of this reflected light depends on the index of refraction of the water and thus is slightly different for different colors. This gives rise to the primary rainbow at about 42 degrees opposite to the direction of sun. (The secondary rainbow corresponds to two internal reflections.) Question: Why can't we see a zeroth order rainbow by looking at rays like C that exit the drop without internal reflections?
(9/99) The problem has been solved by Yevgeny Kats (e-mail yevgenyk@inter.net.il), by David Augier (e-mail augier@irsamc2.ups-tlse.fr), and by Yinon Arieli (e-mail yinonarieli@hotmail.com).
The solution:
Using Snell's law one can easily show that an incoming ray that has an incidence angle (angle between the ray and the radius of the drop, i.e., the normal to the surface) denoted by a will be deflected by an angle b=2[a-arcsin((sin a)/n)], where n is the index of refraction of water (approximately 1.33). Different rays are refracted in different directions. The intensity of the observed light depends on how much light is scattered in a given direction and therefore it depends on the rate at which the angle of deflection changes as the impact parameter of the incoming ray changes. The slower the change, the larger the intensity.
In ordinary (i.e., first or second order) rainbows the derivative db/da vanishes for some value of a. At that (stationary) point the intensity of the light will be maximal. Since that optimal angle depends on n, and the index of refraction depends on color, each color will have slightly different angle of maximal intensity. This is how a regular rainbow is created. (Actually it would be more correct to measure the deflection angle as a function of impact parameter, rather than incidence angle. However, the point at which db/da=0 is obviously also the point at which the derivative with respect to impact parameter vanishes.)
In the zeroth order rainbow the derivative never vanishes. The equation db/da=0 leads to the condition n=1, which cannot be satisfied. Therefore there will be no zeroth order rainbow!
Comment (28/12/01): The mathematics of regular rainbow is nicely explained here.
Comment (14/7/03): Tobias Hackstock brought to our attention that the entire discussion above relies on the fact that we are considering spherical drops. Ice crystals, naturally, produce optical phenomena (such as "sundogs", "halos") detrmined by the fact that the crystal has flat faces, and the direction of transmission depends on the orientation of the crystal. (Consequently, the tranmission will be maximum when transmission angle is stationary as a function of the orientation of the ice crystal.) This web site provides a detailed explanation of several related phenonomena.
 Back to "front page"
Back to "front page"