Discussion of the Question 05/96
The question was:When hockey puck is sliding on the ice it usually performs both linear motion (translation) and rotation. One notices, that the rotation stops exactly at the same moment as the center of mass comes to rest, i.e. the translation ends. Why?
We may assume (approximately) that the motion is slowed down by the "usual solid friction", i.e. the element of puck with mass (dm) which weighs g*(dm) experiences the friction force k*g*(dm) in the direction opposite to the direction of motion of that element.
(10/97) Gil Ariel and Shai Machness from Tel Aviv University wrote down the correct equations describing the motion of puck. They, however, were able to analyze the solution only in the limit of very small linear velocity or very small angular velocity.
(3/99) Eitan Federovsky (e-mail eitan@peach-networks.com) considered a simpler case and reached results which are slightly more susceptible to analysis. Below we present an edited version of his solution. (His equations are essentially the same as equations obtained by Ariel and Machness, but simplified geometry enables to make "one extra step".)
Instead of a disk we consider a ring of radius r and mass m sliding with linear velocity (of the center of mass) v and rotation with angular velocity w. The velocity of each point of the ring is sum of the velocity of center of mass v and velocity of rotation around center of mass (equal to the vector product of angular velocity vector and radius vector. Assume that the center of mass is moving in x-direction. The x component of the force will be
-k*m*g/(2{Pi}) int ((v-w*r*sin(alpha))/sqrt(v2 +(w*r)2 - 2*w*r*v*sin(alpha))
where the integral is performed over all angles alpha. Note that the integrand is simply an x-component of the total velocity of an element of a ring divided by the absolute value of the total velocity. Obviously this force is equal to m*(dv/dt).
Similarly we can calculate the torque. Instead of projecting force on x-axis, we now project it on direction tangential to the circle. The result is
-k*m*g*r/(2{Pi}) int ((w*r-v*sin(alpha))/sqrt(v2 +(w*r)2 - 2*w*r*v*sin(alpha))
which is equal to m*r2(dw/dt). By comparing the expressions for torque and force we immediately see that they are given by function of the same type:
F(x) = int (x-sin(alpha))/sqrt(1+x2-2*x*sin(alpha))
dv/dt=-k*g/(2{Pi})*F(v/w*r)
d(w*r)/dt=-k*g/(2{Pi})*F(w*r/v).
Behavior of the function F is depicted in the following figure both as function of v/w*r and its inverse.
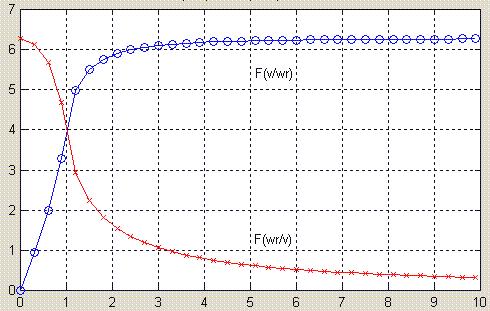
We see that if v is small compared to w*r the force acting to stop v is very small, while the moments on w*r are high, and also in the other way. This is physically explained by noticing that the friction force is only affected by the mass and the direction of the motion!. If w*r is very high and v is small, the total velocity vector direction is influenced mainly by w*r, and when adding we get from symmetry that the total force is zero, while the moments are high. If v is high and w*r is small, the direction of total velocity vector is mainly derived from v, so total velocity vector ~ v and the total force is high, while from symmetry the total moments are small.
(3/99) Y. Kantor: In addition we notice that if we start with v=w*r then d(w*r)/dt=dv/dt and therefore the ratio v/(w*r) will not change with time. Therefore, the rotation and translation will stop simultaneously. It remains to be shown, that whatever the initial ratio (except for trivial cases v=0 or w=0) the final ratio will approach the fixed value v/(w*r)=1! It seems that we passed the conceptually difficult stages of the solution. Nevertheless, there is some hard work ahead. We are waiting for continuation of the solution.
 Back to "front page"
Back to "front page"