Discussion of the Question 10/01
AREA MAXIMIZATION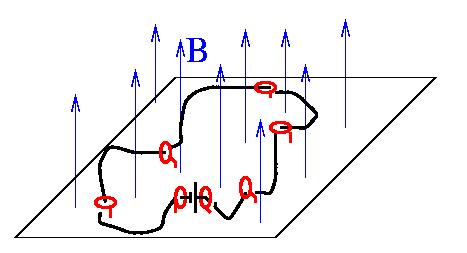
The question was:
A flexible electric wire-loop (of fixed length) (black line in the picture) is placed on a horizontal plane and is free to slide on it. At certain points rings (shown in red) are anchoring the wire to the plane. The wire can slide through the rings. A battery ensures that a constant current is flowing through the ring. Strong magnetic field B is applied perpendicular to the plane.
(a) Show that the wire will assume shape maximizing the area surrounded by the wire (consistent with the constraints imposed by the rings).
(b) What happens if the rings are placed in such a way that they force the current loop to cross itself?
(8/03) Y. Kantor: From the various submitted solutions it became clear to us that the problem was poorly formulated, i.e. the general solution is more complicated than implied in the question. The treatment of a simple "convex polygon" case has been presented (6/6/2002) by Chetan Mandayam Nayakar (e-mail mn_chetan@yahoo.com). His solution was as follows:
Area A of a regular (non-selfintersecting) curve can be calculated using the formula below, where n is the normal to the surface.
A=(1/2){\int}rxdr·n= (1/(2B)){\int}rxdr·B= (1/(2BI))I{\int}rxdr·B= (1/(2BI))M·B
In the second part of the formula we replace n by B/B, where B is the magnetic field, which by the conditions of the problem is perpendicular to the plane. In the third part we multiplied and divided by current I, and noted that the integral is simply the definition of the magnetic moment (in MKSA units) M. We also note, that the expression for the area can be rewritten as A=(1/(2BI))I{\int}Bxdr·r= (1/(2BI))I{\int}dF·r Thus, the area is proportional to the integral of the radial component of the force multiplied by the radius.
We should, however, notice, that the change of the sign of magnetic field would change the above derivation, and actually lead to minimization (rather than maximization) of the area.
Ivan Sirakov Laboratoire de Rheologie des Matieres Plastiques of CNRS, St Etienne (France) (e-mail Yvan.Sirakov@univ-st-etienne.fr) sent us (22/7/03) a detailed solution of the problem which can be seen here in PDF format. The solution considers directly the forces, and demonstrates that equilibrium positions can be minima, maxima or even saddle points. While this not a complete solution (yet), it indicates the complexity of the problem, and nice examples. We do not know whether more general statement about the problem can be made.
 Back to "front page"
Back to "front page"