Answer to the Question 01/01
FLOATING SPHEREThe question was:
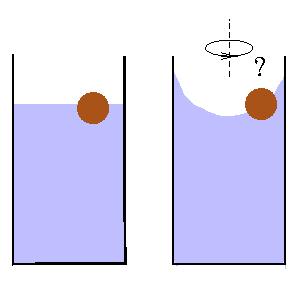
A sphere of uniform density floating in a glass of water (left figure) can be at any distance from the axis of the glass. Where will be the sphere located if the glass is rotating with a constant angular velocity (right figure)?
(9/01) We received a surprisingly large number of wrong solutions of the problem. Indeed it is a bit more complicated than appears at the first glance. So we decided to publish the solution without further delays...
A nice solution of this problem can be found in G.K. Batchelor, An Introduction to Fluid Dynamics, par.1.4 (Cambridge University Press, 1967 (and later)).
Answer: This sphere will float at the center of the surface (i.e. on the axis of symmetry/rotation).
The solution:
The necessary condition for equilibrium of a fluid is the equilibrium between the external ("long-range") force density F and the gradient of the pressure P:
F=grad P.
If the long-range force is be expressed as a product of density d and a (minus) gradient of some potential U then:
-d grad U=grad P.
By taking curl of both sides we get:
(grad d) x (grad U)=0.
Thus levels of constant density and constant potential coincide. In a reference frame rotating with angular velocity w the potential U is given by:
U=gz-(1/2)w2(x2+y2),
where the second term accounts for the centrifugal force. Thus, the equipotential surfaces, and consequently also the surfaces of constant density are paraboloids of rotation, as depicted in the following figure:

Of course, the surface of the liquid is also a paraboloid of rotation. Now, look at the sphere and at the liquid which it displaced. Imagine that the sphere is not there and its place is filled with a liquid. This liquid would be at equilibrium. However, it would NOT be of constant density - it's density would be slightly higher on the right Now if we place a uniform density sphere it's mass distribution is closer to the axis of rotation, and consequently the centrifugal force is smaller that the force from the liquid it expelled (which is equal to the centrifugal force that would apply to the liquid if it would be there), and therefore it would NOT be at equilibrium, but would be driven towards the center. Consequently, at the equilibrium the sphere would float in the center of the surface.
 Back to "front page"
Back to "front page"