Discussion of the Question 10/00
CHARGES ON A CIRCLEThe question was:
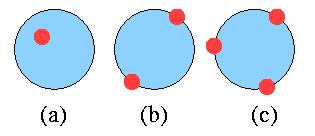
Several identical point charges (shown in red) are placed on a circular disk (shown in blue) so as to minimize the electrostatic energy of the system. Obviously, single charge can be placed anywhere as depicted in Fig. (a), while a pair of charges will occupy opposite sides of the diameter of the circle, as in Fig. (b). Similarly, three charges will form an equilateral triangle, as in Fig. (c). What can you say about the geometric arrangement of 4, 5, 6, ... charges?
(6/11/00) Y. Kantor: We are getting many replies claiming that the optimal placement of the charges is the equidistant placement along the boundary of the disk, i.e. on the circle. This seems to be true for number of charges n=2 or 3. But is it true for larger n? It is possible that equally spread charges represent a local energy minimum. But is it a global minimum? As an example, let us compare configuration of equally spaced charges on the boundary with configuration in which one charge is in the center of the circle while the remaining are equally spaced on the boundaries. Two such configurations are depicted for n=7 below.

The following table presents the energies of those two configurations for various values of n. (It is assumed that those are unit charges and the radius of the circle is also unity.)
n with charge in center without charge in center
3 2.500000000000000 1.732050807568877
4 4.732050807568877 3.828427124746190
5 7.828427124746190 6.881909602355869
6 11.88190960235587 10.96410161513776
7 16.96410161513776 16.13335409673741
8 23.13335409673741 22.43892676967297
9 30.43892676967297 29.92344919779823
10 38.92344919779824 38.62449897970962
11 48.62449897970962 48.57567511970017
12 59.57567511970017 59.80736151791218
13 71.80736151791218 72.34728957471518
14 85.34728957471515 86.22096479601028
15 100.2209647960103 101.4519980160739
16 116.4519980160739 118.0623677300199
17 134.0623677300200 136.0726314193666
18 153.0726314193665 155.5020983001627
19 173.5020983001626 176.3689723517624
20 195.3689723517624 198.6904720782230
You immediately see that for n=12 it is already worthwhile to put one
of the charges in the center, and therefore the configuration where all the
charges are on the boundaries is not the global minimum!
Obviously, we did not intend to find the global minimum. We just tried to demonstrate that equally spaced charges on the boundary, are not necessarily the optimal placement of the charges...
 Back to "front page"
Back to "front page"