Answer to the Question 12/00
COAXIAL CABLEThe question was:
A coaxial cable is built of two parallel metal cylinders of
arbitrary cross-section. If current is flowing in the inner cylinder
and an equal and opposite current is flowing in the outer cylinder,
then magnetic field will be present inside the cable, and one can define
inductance L per unit length of the cable. Similarly, one can charge
the inner and outer cylinders with opposite charges, and view it as a capacitor
with capacitance C per unit length of the cable. Show that expression
(LC)1/2 is independent of the shape of the cross-sections and find
its value.
(5/2001) The problem has been solved correctly by Victor Ivanov (5/12/2000) from the Faculty of Physics, Sofia University, Bulgaria (e-mail vgi@phys.uni-sofia.bg), by Zilong Chen (8/12/2000) from MIT (e-mail zilong), by Zoran Hadzibabic (8/12/2000) from the School of Science at MIT (e-mail zoran@mit.edu), by Ee Hou Yong (14/1/2001) from Stanford University (e-mail eehou@leland.stanford.edu), and by Itzhak Shapir (18/3/2001) (e-mail ishapir1@netvision.net.il).
The answer: 1/c, where c is the speed of light.
The solution: There are several possible approaches to the problem. (The solutions are presented in Gaussian units.)
Solution No. 1:
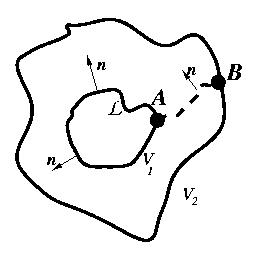
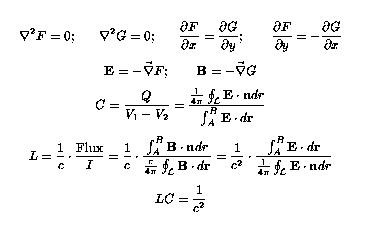
The problems of calculation of C and L (per unit length) are essentially two-dimensional problems. The equations above prove the required statement. Below we explain the proof:
Calculation of capacitance requires solution of two-dimensional electrostatic equation, i.e. finding a harmonic two-dimensional function F(x,y) which has a constant value (say, V1) on the inner surface, and a different constant value (say, V2) on the outer surface. ["Harmonic" means a function with vanishing Laplacian.] The capacitance per unit length of the cable will be determined by Q/(V1-V2), where the charge per unit length Q is determined by the the integral of the normal component of the electric field (grad F) along, say, inner surface, i.e. the (two-dimensional) electric flux, divided by 4{pi}.
In two dimensions any harmonic function F can be treated as a real part of an analytic function. The imaginary part G of the same analytic function will also be a harmonic function representing a potential of a field which is everywhere perpendicular to the field created by the potential F. [See the proof of this property in Ch. 4, of W.K.H. Panofsky and M. Phillips Classical Electricity and Magnetism, Addison-Wesley, 2nd ed. (1972). Of course, the existence of potential G can be also proven directly without introduction of analytic functions.] Moreover the two functions will satisfy Cauchy-Riemann relations: x-derivative of F coincides with y-derivative of G, x-derivative of G coincides with minus y-derivative of F. From these relations, we can directly see that if we choose two points in a two-dimensional plane, the potential difference between the two points calculated using one of the potentials, i.e. integral of a field along some line joining the points, coincides with a flux of the other field through a line joining the points.
One can easily convince himself that grad G represents the magnetic field which we are looking for the calculation of the inductance: In the empty space between the cylinders divergence of the magnetic field is supposed to vanish, which will happen if it is a gradient of a harmonic function. One can also convince himself that this solution satisfies the correct boundary conditions.
Now we note, that according to the Biot-Savart's law the line integral of the magnetic field is [4{pi}/c]I, where I is the current in the inner cylinder. However, as we mentioned in the second paragraph such line integral should be equal to the electric flux of the electrostatic problem. Alternatively, the potential difference in the electrostatic problem is equal the flux of the magnetic field in the magnetic problem. It is this flux which enters the definition of the inductance. [Inductance (per unit length) is flux divided by the current and by c.]
Now we can do a sequence of substitutions: inductance is expressed in terms of magnetic flux and current. Flux can be expressed in terms of voltage difference in electrostatic problem which can be expressed in terms of capacitance and electric flux. The electric flux coincides with line integral of magnetic field, and consequently can be expressed in terms of current. If we execute this sequence of substitutions we see that everything cancels out and we are left with an expression relating the product of capacitance and inductance to the inverse of c2.
Solution No. 2: Solution suggested by Zoran Hadzibabic essentially coincides with the solution described above. However, he chooses a simpler approach. He first considers a case of linear currents and linear charges for which both the electrical and magnetic fields can be easily found and related to each other. In particular, one can easily see that electric and magnetic fields are perpendicular to each other. Now, he "builds" the solution of the problem in question by construction electrostatic problem from linear charges and magnetostatic problem from linear currents and noticing that correct boundary conditions (requiring minimization of energy) are identical for both problems. Consequently, he finds that relation between the product of capacitance and inductance and the speed of light in the general case remain the same as in trivial cases.
Solution No. 3: Solution suggested by Victor Ivanov was very original and different from most of the submitted solutions. First he assumed that an electrostatic problem has been solved and expressed the capacitance via electrostatic energy (i.e., an integral of squared electric field). Then he looked at the same problem from a reference frame moving with small velocity v along the axis of the of the cylinder. To the lowest order in in v/c the relativistic effects do not change the charge density. Thus the current will be simply the charge density multiplied by v. On the other hand, the magnetic field B in the new reference frame will be related to electric field E in the old reference frame by B=vE/c. The transverse dimensions of the cable will not be changed by relativistic effects. We can now use the knowledge of the new magnetic field and the new current to calculate the inductance (e.g., via energy relations) and relate it to the capacitance of the original problem, and to obtained the desired answer.
Solution No. 4: This solution is "a little bit cheating". Nevertheless, it is a valid solution. We first think of the couple of cylinders as a wave-guide. Consider a transverse electromagnetic wave propagating through the guide. For detailed desciption of such waves see, e.g., chapter 8 in J.D. Jackson Classical Electomagnetism, 2nd ed., Wiley, NY (1975). It can be shown that the speed of propagation of such wave is c independently of the cross section of the guide. On the other hand we can view the same problem as a "classical" transmission line problem, of a series of capacitors and inductances, and show that the speed of propagation of the wave is the inverse of the square root of LC. This leads to the desire result. Of course, strictly speaking the "transmission line" treatment is "quasistatic"; however, it will be correct at low frequency, and it is sufficient for us to prove it at any frequency.
Back to "front page"