יחידה 9: רגרסיה וניבוי לינארי  >> 9.1:  רגרסיה וניבוי לינארי

רגרסיה וניבוי לינארי

אחת המטרות של מתאם (r) היא לדעת האם קיים קשר בין שני משתנים. מטרה נוספת בחישוב מתאם בין שני משתנים היא ניבוי.

במידה ומצאנו קשר בין x לבין y, נוכל להשתמש במידע זה על מנת לנבא את ערכי y באמצעות x במדגמים חדשים (בהם נמדוד רק את x).  אנחנו נחליט, בהתאם לצרכים (המחקריים) שלנו, איזה משתנה יהיה המנובא (y), ואיזה יהיה המנבא (x).

לדוגמא: אם מצאנו במדגם מסוים שקיים קשר בין מספר הסיגריות ליום שהאם עישנה במהלך ההיריון לבין משקל העובר, נוכל לנצל ידע זה ולנבא במדגמים אחרים את משקל התינוק ע"פ כמות הסיגריות שהאם מעשנת, לפני הלידה.

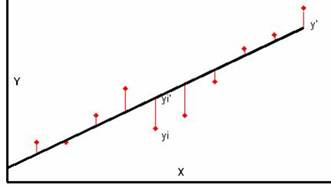
רגרסיה מבוססת על מתאם פירסון. כזכור, מתאם פירסון בוחן האם קיים קשר לינארי בין התצפיות, דהיינו האם התצפיות מסתדרות סביב קו ישר המתאר את הקשר בין x לבין y. כעת נעסוק בקו עצמו, ונשאל מהי נוסחת הקו הזה.

העיקרון על פיו מבוסס קו זה הוא מינימום הריבועים, דהינו הקו אשר יגרום למינימום הסטיות הריבועיות:  (כזכור סכום הסטיות עצמן הוא אפס).

נוסחת הניבוי

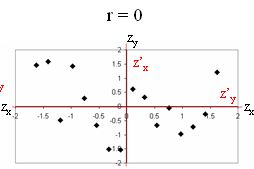
כאשר r=0 אין קשר ביןx  לבין y, לכן המידע על x לא יעזור בניבוי y.

במצב כזה, למדנו בסמסטר הקודם שהערך אשר יגרום למינימום הסטיות הריבועיות  הוא הממוצע.

לכן כאשר r=0, הניבוי יהיה הממוצע (העומד בקריטריון מינימום הריבועים) עבור כל ערכי x,  כלומר שללא קשר לערך ה-x  הניבוי עבור ערך ה-y  יהיה תמיד הממוצע של y. ניתן לראות זאת גם כ-"best guesstimate" משום שאם אנו לא יודעים כלום הודות הקשר שבין x ל-y, הניבוי הטוב ביותר עבור y (הערך שממוצע הסטיות ממנו יהיה הקטן ביותר) יהיה הממוצע:

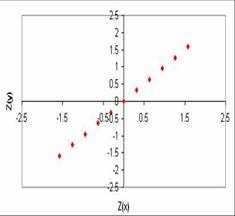
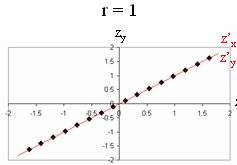
לעומת זאת, כאשר r=1 המתאם מושלם, מכאן שעבור כל נקודה, מידת הקיצוניות ב-y זהה למידת הקיצוניות ב-x לכן:    (כרגע נעבוד רק בציוני תקן, בהמשך נעבור לציונים גולמיים).  בציוני תקן, כאשר r=1, שיפוע הקו יהיה 45 מעלות:

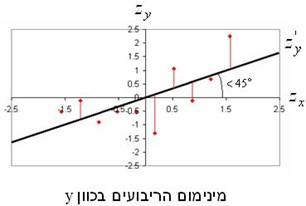
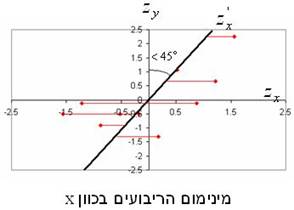
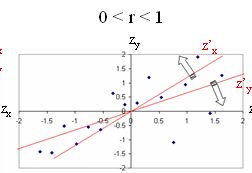
אם המתאם קטן מ-1 (בערכו המוחלט), כלומר נע בין 0 ל-1 או בין 0 לבין -1, שיפוע הקו ינוע בין 0 ל-45 מעלות. השיפוע של קו הניבוי הוא tangent הזווית בין ציר ה-x לבין הקו.

כמו כן ניתן לראות שכשהמתאם קטן מ-1 מידת הקיצוניות של   תהיה קטנה יותר ממידת הקיצוניות של  , זאת באופן פרופורציונאלי למתאם:

באופן כללי נוסחת הניבוי בציוני תקן תהיה: .

כאשר המתאם הוא 0, הציון המנובא של y הוא 0. כאשר המתאם הוא 1, y קיצוני באותה מידה כמו x. כאשר המתאם קטן מ-1 הציון המנובא של y קטן מהציון המנבא של x.

כאמור, למעט המקרים בהם r=1/-1, הציון המנובא של y  פחות קיצוני מאשר ציון x, דהיינו יותר קרוב לממוצע שלו. זאת תופעת הרגרסיה לממוצע (שנדון בה בהמשך) ומכאן השם נוסחת הרגרסיה.

מקור השם מSir Francis Galton- (סטטיסטיקאי חשוב אך חוקר נוראי וגזעני) אשר הבחין שבנים של אנשים גבוהים מאד או נמוכים מאד פחות קיצונים מהוריהם (הדור הבא יותר קרוב לממוצע).

עובדה זו נובעת מכך שבכל ניסוי/תצפית יש לנו טעות במדידה ובממוצע טעות זו היא אפס. כאשר יש תצפית קיצונית, אנו מצפים/מעריכים שהיא מורכבת הן ממרכיב אמיתי והן ממרכיב טעותי ששיחק ל"טובתה".

עקרון מינימום הריבועים מתייחס למשתנה המנובא: כלומר כאשר נבקש לנבא את y מתוך x אנו נחפש מינימום טעויות בכיוון ה-y, לעומת זאת כאשר נרצה לנבא את x על סמך y מינימום הריבועים יהיה בכיוון ה-x. לכן מאחר וניתן לבנות קו רגרסיה ל-y מתוך x, וקו ל-x מתוך y, קיימים שני קווים אפשריים.

הקו שמנבא את y על פי x מתקרב לציר ה-x ואילו הקו שמנבא את x על פי y מתקרב לציר ה-y. בציוני תקן השיפוע של ניבוי y לפי x לכיוון ציר ה-x (הזווית בין הקו לציר ה-x) זהה לשיפוע של קו הניבוי של x לפי y לכיוון ציר ה-y (הזווית בין הקו לציר ה-y).

בציוני תקן, כאשר המתאם שווה 1 או -1, הקווים מתאחדים:

בציוני תקן, כאשר המתאם שווה 0, קווי הניבוי הם בעצם הצירים:

► חזור                    המשך ◄