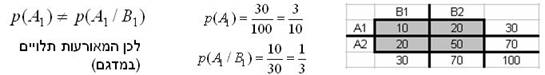|
יחידה 5: חי בריבוע >> 5.4: מבחן חי בריבוע לבדיקת אי-תלות |
|||||||
|
מבחן חי בריבוע לאי-תלות |
|||||||
|
מטרת המבחן: לבדוק האם קיימת תלות סטטיסטית בין 2 משתנים אשר נמדדו בסולם שמי (או סולם גבוה יותר אך בעל "מעט" ערכים). במילים אחרות, האם קיים קשר סטטיסטי בין שני משתנים?
תלות = קשר = מתאם |
|||||||
|
תזכורת: אמרנו ש-2 משתנים הם בלתי תלויים אם , או באופן כללי: עבור כל |
|||||||
|
|
|||||||
|
השאלה הסטטיסטית היא: האם ההבדלים שמצאנו במדגם מספיק גדולים כדי לשכנע אותנו שבאוכלוסייה קיימת תלות בין המשתנים? כי מה שמעניין אותנו הוא האם הפערים שמצאנו והתלות הקיימת בין שני המשתנים קיימים לא רק במדגם אלא גם באוכלוסיה.
ניתן לחשב בכל תא את הערכים הצפויים בהנחת אי-תלות (לפי הערכים שבשוליים), ולאחר מכן לבחון עד כמה הערכים הנצפים סוטים מהערכים הצפויים). |
|||||||
|
תזכורת: A ו-B בלתי תלויים אם או
|
|||||||
|
|||||||
|
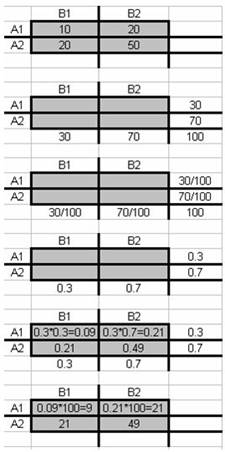
התחלנו עם שכיחויות נצפות בכל תא, וחישבנו שכיחויות צפויות בהנחת אי תלות. הדרך לבדוק האם הפערים שנמצאו במדגם בין הערכים הנצפים לצפויים מספיק גדולים כדי לשכנע אותנו שבאוכלוסייה קיימת תלות בין המשתנים, תהיה שוב חי בריבוע באמצעות אותה נוסחא:
|
|||||||
|
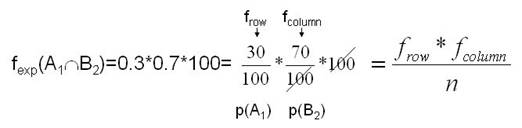
הפעם דרגות החופש תהינה מספר השורות פחות 1 (R-1) כפול מספר העמודות פחות 1 (C-1). לדוגמא במקרה של שניים*שניים דרגות החופש הן 1, דהיינו לאחר שמחשבים exp של תא אחד, יש לנו רק דרך אחת למלא את שאר התאים. בפועל חישוב הערכים הצפויים בכל תא פשוט, בעצם מכפילים את השכיחויות השוליות זו בזו (שכיחות שורה ושכיחות טור) ומחלקים ב- n: |
|||||||
|
בדוגמא שלנו: |
|||||||
|
|
|||||||
|
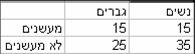
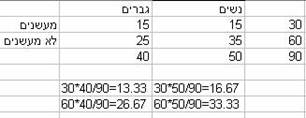
דוגמא: חוקר רצה לבדוק האם קיים קשר בין מין לעישון. מה תהיה החלטתו ברמת בטחון של 95%?
|
|||||||
|
|
|||||||
|
פתרון:
בעצם שואלים האם היחס של המעשנים ללא מעשנים שונה בין נשים לגברים.
נבצע תהליך בדיקת השערות:
1. הנחות: נניח את קיום כל 5 ההנחות של מבחן חי-בריבוע.
2. השערה:
3. רמת מובהקות: , השערה דו-צדדית.
4. בדיקת ההשערה בפועל:
אין אף ערך צפוי קטן מ-5.
נשווה ערך זה לערך הקריטי המתאים בטבלה בשביל לבדוק את מובהקות התוצאה.
ניתן גם לחשב את ה-p-value של הסטטיסטי שקיבלנו:
נסכם את שלב בדיקת ההשערה בפועל:
5. מסקנה: ברמת בטחון של 95% לא נוכל לדחות את ולומר שקיים קשר בין מין לעישון. |
|||||||
|
שימו לב: אם היינו בודקים זאת בסמסטר א' לפי נוסחאות האי-תלות היינו אומרים שקיימת תלות בין המשתנים אך שם לא דיברנו על מובהקות תלות זו. |
|||||||
|
|